cho tam giác MPQ. Lấy N,E lần lượt thuộc MP,MQ. Chứng minh: a, PE<PQ;
b,NE<PQ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
AH
0
Những câu hỏi liên quan
AH
0
16 tháng 3 2022
a, Xét tam giác MDE và tam giác MPQ có
^M _ chung ; \(\frac{MD}{MP}=\frac{ME}{MQ}=\frac{1}{2}\)
Vậy tam giác MDE ~ tam giác MPQ (c.g.c)
\(\frac{MD}{MP}=\frac{DE}{PQ}\Rightarrow DE=\frac{MD.PQ}{MP}=10cm\)
26 tháng 9 2021
Bài 2:
b: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của AB
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
K là trung điểm của GB
I là trung điểm của GC
Do đó: KI là đường trung bình của ΔGBC
Suy ra: KI//BC và \(KI=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra NM//KI và NM=KI
Xét tứ giác NMIK có
NM//KI
NM=KI
Do đó: NMIK là hình bình hành
YK
26 tháng 3 2023
a) xét tam giác MQK vg tại M và tam giác TQK vg tại T có
QK chung
Góc MQK = góc TQK (gt)
=> tam giác MQK = tam giác TQK ( ch.gn)
b) xét tam giác NQK và tam giác PQK có
QK chung
Góc NQK = góc PQK (gt)
QN = QP (gt)
=> tam giác NQK = tam giác PQK (c.g.c)
=> NK = PK
KV
2 tháng 11 2023
Sửa đề:
Cho tam giác MNP cân tại M, điểm Q nằm giữa M và N, lấy điểm E nằm giữa M và P sao cho MQ = PE. Từ Q kẻ đường thẳng song song MP cách NP ở F. Chứng minh:
a) Tứ giác MQFE là hình bình hành
b) Trung điểm của MF thuộc đường thẳng QE
GIẢI
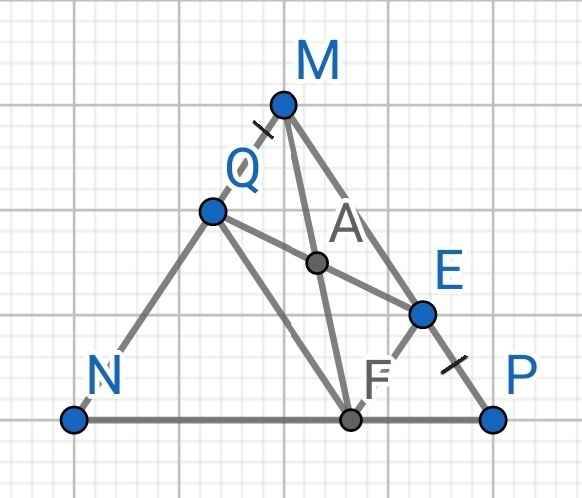
a) Do ∆MNP cân tại M (gt)
⇒ MN = MP
Mà MQ = PE (gt)
⇒ MN - MQ = MP - ME
⇒ QN = ME
Do QF // MP (gt)
⇒ ∠QFN = ∠MPN (đồng vị) (1)
Mà ∆MNP cân tại M
⇒ ∠MPN = ∠MNP
⇒ ∠MPN = ∠QNF (2)
Từ (1) và (2) ⇒ ∠QFN = ∠QNF
⇒ ∆QNF cân tại Q
⇒ QN = QF
Mà QN = ME (cmt)
⇒ QF = ME
Do QF // MP (gt)
⇒ QF // ME
Tứ giác MQFE có:
QF // ME (cmt)
QF = ME (cmt)
⇒ MQFE là hình bình hành
b) Gọi A là trung điểm của MF
Do MQFE là hình bình hành
⇒ A là trung điểm của hai đường chéo MF và QE
⇒ A là trung điểm của QE
⇒ A ∈ QE