Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm
Xét \(\Delta\)ADB có DM là trung tuyến đồng thời là đường cao
=> \(\Delta\)ADB cân tại D
=> \(\widehat{BAD}=\widehat{ABD}\)hay \(\widehat{BAE}=\widehat{ABC}\)
Xét \(\Delta ABC\)và \(\Delta BAE\)có:
AB chung
\(\widehat{ABC}=\widehat{BAE}\left(cmt\right)\)
BC=AE
=> \(\Delta ABC=\Delta BAE\left(cgc\right)\)
a) Xét ΔABC vuông tại A và ΔHCA vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHCA(g-g)
b) Ta có: ΔABC\(\sim\)ΔHCA(cmt)
nên \(\dfrac{AB}{HC}=\dfrac{AC}{AH}=\dfrac{BC}{CA}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{HC}{AH}=1\)
\(\Leftrightarrow HC=AH=2\left(cm\right)\)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC vuông cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(hai cạnh tương ứng)
mà HC=2cm(cmt)
nên HB=2cm
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=8\)
hay \(AB=2\sqrt{2}\left(cm\right)\)
a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC
b: Xét tứ giác BCDE có
A là trung điểm của BD
A là trung điểm của CE
Do đó: BCDE là hình bình hành
Suy ra: BC//DE
Gọi O là tâm đường tròn ngoại tiếp ΔABC
Gọi H là giao của AO với BC
AB=AC
OB=OC
Do đó: AO là trung trực của BC
=>AH là trung trực của BC
=>H là trung điểm của BC
HB=HC=4/2=2cm
Kẻ giao của AO với (O) là D
=>AD là đường kính của (O)
Xét (O) có
ΔABD nội tiếp
ADlà đường kính
Do đó: ΔBAD vuông tại B
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>\(AH^2=6^2-2^2=32\)
=>\(AH=4\sqrt{2}\left(cm\right)\)
Xét ΔBAD vuông tại B có BH là đường cao
nên AB^2=AH*AD
=>\(AD=\dfrac{6^2}{4\sqrt{2}}=\dfrac{9}{\sqrt{2}}\left(cm\right)\)
=>\(R=\dfrac{AD}{2}=\dfrac{9}{2\sqrt{2}}\left(cm\right)\)
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
a.Xét tam giác ABC và tam giác HBA, có:
^B: chung
^BAC = ^BHA = 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA (g.g)
b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)
c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)
\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)
Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)
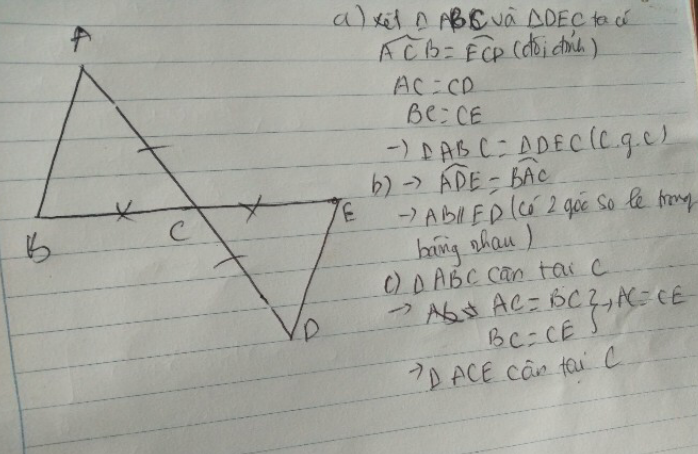
a: Xét ΔABM và ΔADM có
AB=AD
BM=DM
AM chung
Do đó: ΔABM=ΔADM
b: Ta có: ΔABD cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
c: Ta có: \(\widehat{ABD}+\widehat{EBD}=180^0\)
\(\widehat{ADB}+\widehat{BDC}=180^0\)
mà \(\widehat{ABD}=\widehat{ADB}\)
nên \(\widehat{EBD}=\widehat{BDC}\)
Xét ΔAEC có
AB/AE=AD/AC
Do đó: BD//CE
Xét tứ giác BDCE có BD//CE
nên BDCE là hình thang
mà \(\widehat{EBD}=\widehat{BDC}\)
nên BDCE là hình thang cân
Suy ra: DE=BC