Giúp mình giải bài này với mọi người ơi
Giải phương trình:
\(x^4+\sqrt{x^2+2016}=2016\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
6
BD
13 tháng 1 2017
( 15-x ) + 2x = 2016-4
( 15-x ) + 2x = 2012
15-x + 2x = 2012
Vì - x + 2x = x nên có :
15 + x = 2012
x = 2012 - 15
x = 1997
13 tháng 1 2017
(15-x)+2x=2016-2
(15-x)+2x=2012
15x1-Xx1=2012
1(15-x)=2012
15-x=2012:1
15-x=2012=>x=15-2012=-1997
10 tháng 12 2021
\(a,PT\Leftrightarrow x^2-3x+2+x^2-x\sqrt{3x-2}=0\left(x\ge\dfrac{2}{3}\right)\\ \Leftrightarrow\left(x^2-3x+2\right)+\dfrac{x\left(x^2-3x+2\right)}{x+\sqrt{3x-2}}=0\\ \Leftrightarrow\left(x^2-3x+2\right)\left(1+\dfrac{x}{x+\sqrt{3x-2}}\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)\left(1+\dfrac{x}{x+\sqrt{3x-2}}\right)=0\)
Vì \(x\ge\dfrac{2}{3}>0\Leftrightarrow1+\dfrac{x}{x+\sqrt{3x-2}}>0\)
Do đó \(x\in\left\{1;2\right\}\)
10 tháng 12 2021
\(b,ĐK:0\le x\le4\\ PT\Leftrightarrow x+2\sqrt{x}+1=6\sqrt{x}-3-\sqrt{4-x}\\ \Leftrightarrow x-4\sqrt{x}+4=-\sqrt{4-x}\\ \Leftrightarrow\left(\sqrt{x}-2\right)^2=-\sqrt{4-x}\)
Vì \(VT\ge0\ge VP\Leftrightarrow VT=VP=0\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{4-x}=0\end{matrix}\right.\Leftrightarrow x=4\left(tm\right)\)
Vậy PT có nghiệm \(x=4\)
HT
22 tháng 2 2016
™Ta có: C=(x^2-1)(x^2-2)...(x^2-2006)
™Thay x=5 vào biểu thức C ta được :
™C=(5^2-1)(5^2-2)...(x^2-2016)=(25-1)(25-2)...(25-1016)=(25-1)(25-2)(25-3)(25-4)...(25-5)...(25-2016)=(25-1)(25-2)(25-3)(25-4)...(0)...(25-2016)
™Vì 0 nhân với số nào cũng bằng 0 nên C=0
™Vậy biểu thức C có giá trị bằng 0 tại x=5
--------------------------
™
HP
22 tháng 2 2016
(x^2-1)(x^2-2)...(x^2-2016)
để ý ta thấy C=(x^2-1)(x^2-2)...(x^2-25)...(x^2-2016)
thay x=5 vào ta có
C=(5^2-1)(5^2-2)...(5^2-25)...(5^2-2016)
C=(5^2-1)(5^2-2)....0...(5^2-2016)=0
vậy C=0
6 tháng 10 2020
Xét: \(\sqrt{1+n^2+\frac{n^2}{\left(n+1\right)^2}}=\sqrt{\frac{\left(n+1\right)^2+n^2\left(n+1\right)^2+n^2}{\left(n+1\right)^2}}\) (với \(n\inℕ\))
\(=\sqrt{\frac{n^2+2n+1+n^4+2n^3+n^2+n^2}{\left(n+1\right)^2}}\)
\(=\sqrt{\frac{n^4+n^2+1+2n^3+2n^2+2n}{\left(n+1\right)^2}}\)
\(=\sqrt{\frac{\left(n^2+n+1\right)^2}{\left(n+1\right)^2}}=\frac{n^2+n+1}{n+1}=n+\frac{1}{n+1}\)
Áp dụng vào ta tính được: \(\sqrt{1+2015^2+\frac{2015^2}{2016^2}}+\frac{2015}{2016}=2015+\frac{1}{2016}+\frac{2015}{2016}\)
\(=2015+1=2016\)
Khi đó: \(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=2016\)
\(\Leftrightarrow\left|x-1\right|+\left|x-2\right|=2016\)
Đến đây xét tiếp các TH nhé, ez rồi:))
TA
6 tháng 10 2020
chẳng biết đúng ko,mới lớp 5
\(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=\sqrt{1+2015^2+\frac{2015^2}{2016^2}}+\frac{2015}{2016}\)
\(\sqrt{x^2}-\sqrt{2x}+\sqrt{1}+\sqrt{x^2}-\sqrt{4x}+\sqrt{4}=\sqrt{1}+\sqrt{2015^2}+\sqrt{\frac{2015^2}{2016^2}}+\frac{2015}{2016}\)
\(\sqrt{x^2}-\sqrt{6x}+3=1+2015+\frac{2015}{2016}+\frac{2015}{2016}\)
\(x-\sqrt{6x}=1+\frac{2015}{1+2016+2016}-3\)
\(x-\sqrt{6x}=2-\frac{2015}{4033}\)
\(x-\sqrt{6x}=\frac{6051}{4033}\)
21 tháng 3 2019
\(\sqrt{x-2016}+\sqrt{y-2017}+\sqrt{z-2018}+3024=\frac{1}{2}\left(x+y+z\right)\)
\(\Leftrightarrow2\left(\sqrt{x-2016}+\sqrt{y-2017}+\sqrt{z-2018}+3024\right)=x+y+z\)
\(\Leftrightarrow2\sqrt{x-2016}+2\sqrt{y-2017}+2\sqrt{z-2018}+6048=x+y+z\)
\(\Leftrightarrow x-2\sqrt{x-2016}+y-2\sqrt{y-2017}+z-2\sqrt{z-2018}+6048=0\)
\(\Leftrightarrow x-2016-2\sqrt{x-2016}+1+y-2017+2\sqrt{y-2017}+1+z-2018-2\sqrt{z-2018}+1=0\)
\(\Leftrightarrow\left(\sqrt{x-2016}-1\right)^2+\left(\sqrt{y-2017}-1\right)^2+\left(\sqrt{z-2018}-1\right)^2=0\)
\(ĐK:x\ge2016;y\ge2017;z\ge2018\)
\(\Leftrightarrow\hept{\begin{cases}\sqrt{x-2016}-1=0\\\sqrt{y-2017}-1=0\\\sqrt{z-2018}-1=0\end{cases}\Leftrightarrow\hept{\begin{cases}\sqrt{x-2016}=1\\\sqrt{y-2017}=1\\\sqrt{z-2018}=1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=2017\\y=2018\\z=2019\end{cases}}}\)
2T
22 tháng 8 2019
\(\sqrt{x^2+4}-2\sqrt{x+2}=0\)
\(\Leftrightarrow\sqrt{x^2+4}=2\sqrt{x+2}\)
\(\Leftrightarrow\sqrt{x^2+4}=\sqrt{4x+8}\)
\(\Leftrightarrow\sqrt{x^2+4}^2=\sqrt{4x+8}^2\)
\(\Leftrightarrow x^2+4=4x+8\)
\(\Leftrightarrow x^2-4x-4=0\)
\(\Delta=\left(-4\right)^2-4.1.\left(-4\right)=16+16=32\)
Vậy \(x_1=\frac{4+\sqrt{32}}{2}\);\(x_2=\frac{4-\sqrt{32}}{2}\)
P/S: Ko chắc
22 tháng 8 2019
\(\sqrt{x^2+4}-2\sqrt{x+2}=0.\)
\(\Rightarrow\sqrt{x^2+4}=2\sqrt{x+2}\)
\(\Rightarrow x^2+4=2x+4\)
\(\Rightarrow x^2+4-2x-4=0.\)
\(\Rightarrow x^2-2x=0\)
\(\Rightarrow x\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-2=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}}\)
Vậy .............
Study well
5 tháng 10 2021
a, TK: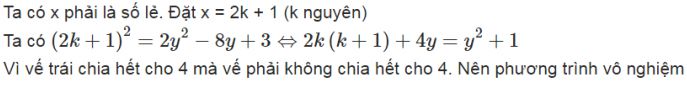
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương
20 tháng 2 2022
Bài 8:
a: Khi a=1 thì phương trình sẽ là \(\left(1-4\right)x-12x+7=0\)
=>-3x-12x+7=0
=>-15x+7=0
=>-15x=-7
hay x=7/15
b: Thay x=1 vào pt, ta được:
\(a^2-4-12+7=0\)
\(\Leftrightarrow\left(a-3\right)\left(a+3\right)=0\)
hay \(a\in\left\{3;-3\right\}\)
c: Pt suy ra là \(\left(a^2-16\right)x+7=0\)
Để phương trình đã cho luôn có một nghiệm duy nhất thì (a-4)(a+4)<>0
hay \(a\notin\left\{4;-4\right\}\)