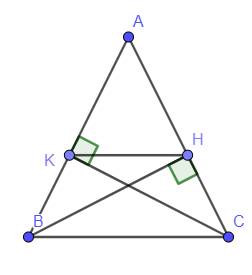
Cho tam giác ABC cân tại A . Kẻ BH vuông góc với AC tại H , CK vuông góc với AB tại K . Chứng minh rằng :
a/ △ABH=△ACK
b/ △AHK cân
c/ KH // BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 2 2023
`a)`
Có `Delta ABC` cân tại `A=>AB=AC`
Xét `Delta ABH` và `Delta ACK` có :
`hat(AHB)=hat(AKC)(=90^0)`
`hat(A)-chung`
`AB=AC(cmt)`
`=>Delta ABH=Delota ACK(c.h-g.n)`
`b)`
Xét `Delta BHC` và `Delta CKB` có :
`hat(BHC)=hat(CKB)(=90^0)`
`hat(KBC)=hat(HCB)(hat(ABC)=hat(ACB))`
`BC-chung`
`=>Delta BHC=Delta CKB(c.h-g.n)`
`c)`
Có `Delta ABH= Delta ACK(cmt)=>AH=AK` ( 2 cạnh t/ứng )
`=>Delta AHK` cân tại `A=>hat(AHK)=(180^0-hat(A))/2`
`Delta ABC ` cân tại `A=>hat(ACB)=(180^0-hat(A))/2`
mà `2` góc này ở vị trí đ/vị
nên `KH//BC`
28 tháng 2 2023
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K co
AB=AC
góc A chung
=>ΔAHB=ΔAKC
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKCB=ΔHBC
c: Xét ΔABC có AK/AB=AH/AC
nên KH//CB
2 tháng 1 2023
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: ΔAHB=ΔAKC
=>AH=AK
c: Xét ΔAKI vuông tại K và ΔAHI vuông tại H co
AI chung
AH=AK
Do đó: ΔAKI=ΔAHI
=>góc KAI=góc HAI
=>AI là phân giác của góc BAC
9 tháng 3 2022
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK
b: Xét ΔOBK vuông tại K và ΔOCH vuông tại H có
KB=HC
\(\widehat{KBO}=\widehat{HCO}\)
Do đó:ΔOBK=ΔOCH
27 tháng 1
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC
b: Ta có: ΔAHB=ΔAKC
=>AH=AK và \(\widehat{ABH}=\widehat{ACK}\)
Ta có: AH+HC=AC
AK+KB=AB
mà AH=AK và AC=AB
nen HC=KB
Xét ΔOKB vuông tại K và ΔOHC vuông tại H có
KB=HC
\(\widehat{KBO}=\widehat{HCO}\)
Do đó: ΔOKB=ΔOHC
c: ta có; ΔOKB=ΔOHC
=>OB=OC
=>O nằm trên đường trung trực của BC(1)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
ta có: IB=IC
=>I nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,I thẳng hàng
9 tháng 5 2023
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
góc A chung
=>ΔABH=ΔACK
b: góc KBC+góc ICB=90 độ
góc IBC+góc HCB=90 độ
mà góc KBC=góc HCB
nên góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC
28 tháng 4 2023
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB chung
=>ΔAHB=ΔAKC
=>AH=AK
b:
Xét ΔABC có
BH,CK là đường cao
BH cắt CK tại I
=>I là trực tâm
=>AI vuông góc BC tại M
Xét ΔKBC vuông tạiK và ΔHCB vuông tại H có
BC chung
KC=HB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác
c: Xet ΔBAC có AK/AB=AH/AC
nên KH//BC
4 tháng 2 2021
a) Xét ΔBHC vuông tại H và ΔCKB vuông tại K có
CB chung
\(\widehat{BCH}=\widehat{CBK}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBHC=ΔCKB(cạnh huyền-góc nhọn)
b) Ta có: ΔBHC=ΔCKB(cmt)
nên HC=KB(hai cạnh tương ứng)
Ta có: AK+KB=AB(K nằm giữa A và B)
AH+HC=AC(H nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và KB=HC(cmt)
nên AK=AH
Xét ΔAKH có AK=AH(cmt)
nên ΔAKH cân tại A(Định nghĩa tam giác cân)
c) Ta có: ΔAKH cân tại A(cmt)
nên \(\widehat{AKH}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAKH cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AKH}=\widehat{ABC}\)
mà \(\widehat{AKH}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên HK//BC(Dấu hiệu nhận biết hai đường thẳng song song)
d) Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK(cạnh huyền-góc nhọn)
nên \(\widehat{ABH}=\widehat{ACK}\)(hai góc tương ứng)
hay \(\widehat{KBO}=\widehat{HCO}\)
Xét ΔKBO vuông tại K và ΔHCO vuông tại H có
KB=HC(cmt)
\(\widehat{KBO}=\widehat{HCO}\)(cmt)
Do đó: ΔKBO=ΔHCO(cạnh góc vuông-góc nhọn kề)
nên OB=OC(hai cạnh tương ứng)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Từ (3), (4) và (5) suy ra A,O,M thẳng hàng(đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2023
Do \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{BCA}=\widehat{CBA}\) hay \(\widehat{BCH}=\widehat{CBA}\)
Xét hai tam giác vuông BHC và CKB có:
\(\left\{{}\begin{matrix}BC\text{ chung}\\\widehat{BCH}=\widehat{CBK}\end{matrix}\right.\) \(\Rightarrow\Delta_VBHC=\Delta_VCKB\left(ch-gn\right)\)
\(\Rightarrow CH=BK\) (1)
Mà \(\Delta ABC\) cân tại A \(\Rightarrow AB=AC\)
\(\Rightarrow AK+BK=AH+CH\) (2)
(1);(2) \(\Rightarrow AK=AH\)
\(\Rightarrow\Delta AHK\) cân tại A
mik cần gấp nha cứu mik
còn bạn nào hcoj giỏi thức ko huhu :((
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABH=ΔACK
b: Xét ΔAHK có AH=AK(ΔABH=ΔACK)
nên ΔAHK cân tại A
c: Xét ΔABC có
AK/AB=AH/AC
Do đó: KH//BC