Bài 11. Cho điểm A nằm ngoài đường tròn (O). Kẻ các tiếp tuyến AB, AC với (O) (B,C là
các tiếp điểm). AO cắt BC tại H. Kẻ đường kính BD của (O). Chứng minh rằng:
a) AO ∥ CD.
b) AB2 = AC2 = AH · AO
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

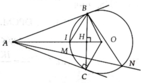
a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trực của BC
hay OA⊥BC

a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
b: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔDBA vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(3\right)\)
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(4\right)\)
Từ (3) và (4) suy ra \(AE\cdot AD=AH\cdot AO\)
c: Xét ΔOKA vuông tại K và ΔOHF vuông tại H có
\(\widehat{KOA}\) chung
Do đó: ΔOKA đồng dạng với ΔOHF
=>\(\dfrac{OK}{OH}=\dfrac{OA}{OF}\)
=>\(OH\cdot OA=OK\cdot OF\left(5\right)\)
Xét ΔOCA vuông tại C có CH là đường cao
nên \(OH\cdot OA=OC^2=R^2=OD^2\left(6\right)\)
Từ (5)và (6) suy ra \(OK\cdot OF=OD^2\)
=>\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)
Xét ΔOKD và ΔODF có
\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)
\(\widehat{KOD}\) chung
Do đó: ΔOKD đồng dạng với ΔODF
=>\(\widehat{OKD}=\widehat{ODF}=90^0\)
=>FD là tiếp tuyến của (O)




a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
hay AO⊥BC(1)
Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
hay BC⊥CD(2)
Từ (1) và (2) suy ra AO//DC
b: Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2=AC^2\)