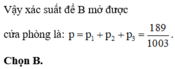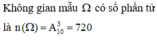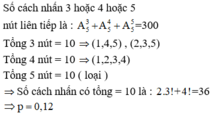một phòng thí nghiệm được bảo vệ và một bảng điều khiển điện tử mở cửa từ xa bản gồm 10 nút bấm đánh số từ 0 đến 9 và một màn hình hiển thị 6 ô trống để nhập password biết rằng để mở vào được phòng thí nghiệm người ta phải bấm 6 nút khác nhau theo quy luật 6 số trên 6 nút tạo thành một số tự nhiên lẻ và lớn hơn 500.000 .Một người không biết quy luật trên đã nhấn ngẫu nhiên liên tiếp 6 nút khác nhau Tính xác suất để người này mở được cửa phòng thí nghiệm đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số cách chọn 3 nút để ấn là A 10 3 = 720 .
Số trường hợp đạt yêu cầu là: (0, 1, 9); (0, 2, 8); (0, 3, 7); (0, 4, 6); (1, 2, 7); (1, 3, 6);
(1, 4, 5) ; (2, 3, 5).
Xác xuất để B mở được cửa là 8/720 = 1/90.

Không gian mẫu: \(C_{10}^3=120\)
Ta có 8 dãy số thỏa mãn đề bài: (0;1;9);(0;2;8);(0;3;7);(0;4;6),(1;2;7);(1;3;6);(1;4;5);(2;3;5)
Xác suất:
\(P=\dfrac{8}{120}+\left(1-\dfrac{8}{120}\right).\dfrac{8}{119}+\left(1-\dfrac{8}{120}\right).\left(1-\dfrac{8}{119}\right).\dfrac{8}{118}=...\)

Công ty X thiết kế bảng điều khiển điện tử để mở hoặc khóa cửa một ngôi nhà. Bảng gồm 5 nút, mỗi nút được ghi một số từ 1 đến 5 và không có hai nút nào được ghi cùng một số. Để mở được cửa cần nhấn liên tiếp ít nhất 3 nút khác nhau sao cho tổng của các số trên các nút đó bằng 10. Một người không biết quy tắc mở cửa trên, đã nhấn ngẫu nhiên liên tiếp ít nhất 3 nút khác nhau trên bảng điều khiển. Xác suất P để người đó mở được cửa ngôi nhà là
A. P = 0,17.
B. P = 0,7.
C. P = 0,12.
D. P = 0,21.