Câu 45: Với góc nhọnα và β tuỳ ý và α < β ta có :
A.cosα - cosβ >0 ; B. cosα - cosβ = 0;
C. cosα - cosβ< 0 ; D. cosα - cosβ > 0 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
7 tháng 9 2023
\(sin\alpha=cos\beta=\dfrac{AB}{BC}\)
\(tan\alpha=cot\beta=\dfrac{AB}{AC}\)
8 tháng 9 2023
\(\alpha+\beta=90^o\)
\(\Rightarrow\beta=90^o-\alpha\)
Theo đề bài :
\(sin\alpha=cos\beta\)
\(\Rightarrow sin\alpha=cos\left(90^o-\alpha\right)\)
mà \(\alpha;90^o-\alpha\) là 2 góc phụ nhau
\(\Rightarrow cos\left(90^o-\alpha\right)=sin\alpha\left(dpcm\right)\)
Tương tự \(tan\alpha=cot\beta=cot\left(90^o-\alpha\right)\)
TN
0
CM
28 tháng 8 2017
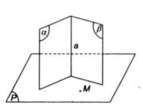
Vậy (MHK) chính là mặt phẳng đi qua M và vuông góc với (α) và (β).
Kết quả: Mặt phẳng (P) cần dựng (tức mp(MHK)) là mặt phẳng đi qua M và vuông góc với Δ.
Vì qua một điểm chỉ có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước nên (P) là duy nhất.
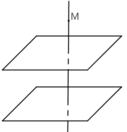
Nếu (α) // (β) thì qua M ta chỉ có thể vẽ một đường thẳng Δ vuông góc với (α) và (β). Bất kì mặt phẳng (P) nào chứa Δ cũng đều vuông góc với (α), (β). Trường hợp này, qua M có vô số mặt phẳng vuông góc với (α), (β).
CM
21 tháng 3 2019
* Ta có sin 2 α + cos 2 α = 1 ⇒ sin 2 α + 16 25 = 1 ⇒ sin 2 α = 9 25
Mà sin α < 0 ⇒ sin α = - 3 5
* Vì sin 2 β + cos 2 β = 1 ⇒ 9 16 + cos 2 β = 1 ⇒ c o s 2 β = 7 16
cos β > 0 ⇒ cos β = 7 4
* sin α + β = sin α . cos β + c o s α . sin β = - 3 5 . 7 4 + 4 5 . 3 4 = 12 - 3 7 20
QT
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có α + β = π nên sinα = sin(π – α) = sinβ, suy ra sin2α = sin2β.
a) A = sin2α + cos2β = sin2β + cos2β = 1.
b) Ta có α + β = π nên cosα = – cos(π – α) = – cosβ.
Khi đó, B = (sinα + cosβ)2 + (cosα + sinβ)2
= (sinβ + cosβ)2 + (– cosβ + sinβ)2
= (sinβ + cosβ)2 + (sinβ – cosβ )2
= sin2β + 2sinβ cosβ + cos2β + sin2β – 2sinβ cosβ + cos2β
= 2(sin2β + cos2β)
= 2 . 1 = 2.
Chọn A
Vì 0 độ<α<β<90 độ nên:
0<sinα<sinβ, cosα>cosβ>0
0<tanα<tanβ, cotα>cotβ>0
=>cosα<cosβ => cosα-cosβ<0 => chọn C.