3A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(3a-1\right)\left(9a^2+3a+1\right)-\left(3a+1\right)\left(9a^2-3a+1\right)+2a+2\)
\(=27a^3-1-\left(27a^3+1\right)+2a+2=27a^3-1-27a^3-1+2a+2\)
\(=-2+2a+2=2a\)

Lời giải:
Ta có:
\(\frac{\tan ^3a}{\sin ^2a}-\frac{1}{\sin a\cos a}+\frac{\cot ^3a}{\cos ^2a}=\frac{\tan ^3a\cos ^2a+\cot ^3a\sin ^2a}{\sin ^2a\cos ^2a}-\frac{\sin a\cos a}{\sin ^2a\cos ^2a}\)
\(=\frac{\frac{\sin ^3a}{\cos ^3a}.\cos ^2a+\frac{\cos ^3a}{\sin ^3a}.\sin ^2a}{\sin ^2a\cos ^2a}-\frac{\sin a\cos a}{\sin ^2a\cos ^2a}\)
\(=\frac{\frac{\sin ^3a}{\cos a}+\frac{\cos ^3a}{\sin a}-\sin a\cos a}{\sin ^2a\cos ^2a}=\frac{\sin ^4a+\cos ^4a-\sin ^2a\cos ^2a}{\sin ^3a\cos ^3a}\)
\(=\frac{(\sin ^2a+\cos ^2a)(\sin ^4a+\cos ^4a-\sin ^2a\cos ^2a)}{\sin ^3a\cos ^3a}\)
\(=\frac{\sin ^6a+\cos ^6a}{\sin ^3a\cos ^3a}=\frac{\sin ^3a}{\cos ^3a}+\frac{\cos ^3a}{\sin ^3a}=\tan ^3a+\cot ^3a\)
Ta có đpcm.

Lướt qua rồi! không phải bạn k mà ấn tượng "đừng lướt qua"
\(A=\frac{3a}{4.1}+\frac{3a}{7.4}+\frac{3a}{10.7}+\frac{3a}{13.10}+..+\frac{3a}{22.19}+\frac{3a}{25.22}=\frac{48}{25}\)
\(a.\left(\frac{3}{4.1}+\frac{3}{7.4}+\frac{3}{10.7}+\frac{3}{13.10}+..+\frac{3}{22.19}+\frac{3}{25.22}\right)=\frac{48}{25}\)
\(B=\left(\frac{3}{4.1}+\frac{3}{7.4}+\frac{3}{10.7}+\frac{3}{13.10}+..+\frac{3}{22.19}+\frac{3}{25.22}\right)\)
\(B=\frac{1}{1}-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+..+\frac{1}{22}-\frac{1}{25}\)
\(B=\frac{1}{1}-\frac{1}{25}=\frac{24}{25}\)
\(A=a.B=\frac{24a}{25}=\frac{48}{25}\Rightarrow a=2\)
\(\frac{3a}{4}+\frac{3a}{28}+\frac{3a}{70}+...+\frac{3a}{418}+\frac{3a}{550}=\frac{48}{25}\)
\(\Rightarrow a\left(\frac{3}{1.4}+\frac{3}{4.7}+\frac{3}{7.10}+...+\frac{3}{19.22}+\frac{3}{22.25}\right)=\frac{48}{25}\)
\(\Rightarrow a\left(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+...+\frac{1}{19}-\frac{1}{22}+\frac{1}{22}-\frac{1}{25}\right)=\frac{48}{25}\)
\(\Rightarrow a\left(1-\frac{1}{25}\right)=\frac{48}{25}\)
\(\Rightarrow a.\frac{24}{25}=\frac{48}{25}\)
\(\Rightarrow a=2\)

VT = sin3a.cos^3a + sin^3a.cos3a
= sin3a.cosa.cos^2a + sin^2a.sina.cos3a
= 1/2.(sin2a + sin4a).cos^2a + 1/2.sin^2a.(sin(-2a) + sin4a)
= 1/2.(sin2a + sin4a).cos^2a + 1/2.sin^2a.(sin4a - sin2a)
= 1/2.sin2a.cos^2a + 1/2.sin4a.cos^2a + 1/2.sin^2a.sin4a - 1/2.sin^2a.sin2a
= 1/2.sin2a.(cos^2a - sin^2a) + 1/2.sin4a.(cos^2a + sin^2a)
= 1/2.sin2a.cos2a + 1/2.sin4a
= 1/4.sin4a + 1/2.sin4a
= 3/4.sin4a = VP
=> đpcm
P/s: Chỉ sợ you ko hiểu

Ta có: \(tan\alpha=3=\frac{sin\alpha}{cos\alpha}\Rightarrow sin\alpha=3cos\alpha\)
Suy ra: \(B=\frac{\left(sin\alpha-cos\alpha\right)\left(sin^2\alpha+cos^2\alpha+sin\alpha.cos\alpha\right)}{\left(sin\alpha+cos\alpha\right)\left(sin^2\alpha+cos^2\alpha-sin\alpha.cos\alpha\right)}\)
\(=\frac{2cos\alpha.\left(1+3cos^2\alpha\right)}{4cos\alpha.\left(1-3cos^2\alpha\right)}=\frac{1+3cos^2\alpha}{2.\left(1-3cos^2\alpha\right)}\)
Tìm tất cả các cặp số tự nhiên (a,b) thỏa mãn (3a - 1) (3a - 2) (3a - 3) (3a - 4) = (2018b + 358799)

\(\left(3^a-1\right)\left(3^a-2\right)\left(3^a-3\right)\left(3^a-4\right)=\left(2018^b+358799\right)\)
Với \(a=0\)dễ thấy không thỏa.
Với \(a>0\)có VT là tích của bốn số tự nhiên liên tiếp nên chia hết cho \(4\).
VP nếu \(b>0\)thì VP là số lẻ nên không chia hết cho \(4\)nên \(b=0\).
Suy ra \(\left(3^a-1\right)\left(3^a-2\right)\left(3^a-3\right)\left(3^a-4\right)=358800\)
Có \(358800=23.24.25.26\)suy ra \(3^a-1=26\Leftrightarrow a=3\).
Vậy phương trình có nghiệm nguyên duy nhất là \(\left(a,b\right)=\left(3,0\right)\).
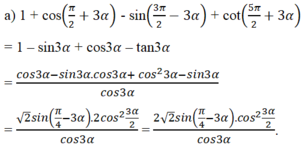
Sao vậy em? Em học lớp 3A à hay cần giúp gì à em?
????????????????????????????3A