tìm x y z thuoc z biet 52/9 = 5+1/x+1/y+1/2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


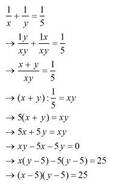
Ta xét:
\(\left(x-5\right)\left(y-5\right)=25\Leftrightarrow x-5=y-5=5\Leftrightarrow x=y=10\)
\(x-5=y-5=-5\Leftrightarrow x=y=0\)
\(\left\{{}\begin{matrix}x-5=1\\y-5=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=30\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=-1\\y-5=-25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\y=-20\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=25\\y-5=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=30\\y=6\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x-5=-25\\y-5=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-20\\y=4\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(10;10\right),\left(0;0\right),\left(6;30\right),\left(4;-20\right),\left(30;6\right),\left(-20;4\right)\right\}\)

Rút gọn thừa số chung
Đơn giản biểu thức
Giải phương trình
Rút gọn thừa số chung
Giải phương trình

Có 2 Th | x-2| , (x-y+1)^2 =0
| x-2| , (x-y+1)^2 là hai số đối ; lx-2/ nguyên dương => ( x - y + 1 )^2 là số nguyên âm
TH1 | x-2| , (x-y+1)^2 =0
=> x = 2 để /x-2/ = 0
thay vào bên kia ta có : ( 2 - y + 1 ) ^2 = 0 => 2 - y + 1 = 0 => 3 - y = 0 => y = 3
TH2 : Tự xét nha bn

P/s : Lớp 7 nha bạn :
Ta có :
\(\frac{x}{12}=\frac{y}{9}=\frac{z}{5};x+y+z=52\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
\(\frac{x}{12}=\frac{y}{9}=\frac{z}{5}=\frac{x+y+z}{12+9+5}=\frac{52}{26}=2\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{12}=2\\\frac{y}{9}=2\\\frac{z}{5}=2\end{cases}\Rightarrow\hept{\begin{cases}x=2.12=24\\y=2.9=18\\z=2.5=10\end{cases}}}\)
Vậy \(x=24;y=18;z=10\)
~ Ủng hộ nhé
Có \(\frac{x}{12}\) = \(\frac{y}{9}\) = \(\frac{z}{5}\) và x + y + z = 52
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có :
\(\frac{x}{12}\) = \(\frac{y}{9}\) = \(\frac{z}{5}\) = \(\frac{x+y+z}{12+9+5}\) = \(\frac{52}{26}\) = 2
+, \(\frac{x}{12}\) = 2 \(\Rightarrow\) x= 24
+, \(\frac{y}{9}\) = 2 \(\Rightarrow\) y = 18
+, \(\frac{z}{5}\) = 2 \(\Rightarrow\) z = 10
Vậy ...
