Bài 4: cho tam giác cân ABC nội tiếp đường tròn (O), cung nhỏ BC có số đo bằng 1000. Tia AO cắt cung nhỏ AC ở E.
a, Tính số đo các góc ở tâm BOE, COE
b, Tính số đo các cung nhỏ AB, AC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TP
Trần Phương Anh
10 tháng 1 2022
Đúng(0)
Những câu hỏi liên quan
27 tháng 5 2021
khi tia OA cắt đường tròn tâm O tại D nên AD là đường kính chia ra 2 cung AD bằng nhau
mà tam giác ABC cân tại A có góc ABC =góc ACB là 2 góc nội tiếp chắc 2 cung AB và AC nên cung AB=cung AC
cung AD=cung AB+cung BD
cung AD=cung AC+cung CD
ta có cung AD=cung AD,cung AB=AC=>cung BD=cung CD
theo đề bài số đo cung nhỏ BD=cung BD+cung CD=>100=2 cung CD=>cung CD bằng 50 độ
MÀ GÓC COD là góc ở tâm chắc cung CD
NÊN SUY RA ĐƯỢC GÓC COD BẰNG 50 ĐỘ
31 tháng 12 2022
Sửa đề: cắt cug nhỏ BC tại E
a:
ΔABC cân tại A
nên AB=AC
mà OB=OC
nên AO là đường trung trực của BC
=>AE là đường kính của (O)và AO là phân giác của góc BAC
sđ cung BC=100 độ
=>góc BAC=50 độ
góc BAE=góc BAC/2=50/2=25 độ
=>góc BOE=2*25=50 độ
=>góc COE=50 độ
b: góc ABC=góc ACB=(180-50)/2=130/2=65 độ
=>sđ cung AB=sđ cung AC=2*65=130 độ
AH
Akai Haruma
Giáo viên
9 tháng 12 2023
Lời giải:
Ta có:
$x+10^0+x+20^0+x+30^0=360^0$
$\Rightarrow 3x+60^0=360^0$
$\RIghtarrow x=100^0$
$\widehat{ABC}=\frac{1}{2}\text{sđc(AC)}=\frac{1}{2}(x+30^0)=\frac{1}{2}(100^0+30^0)=65^0$
$\widehat{ACB}=\frac{1}{2}\text{sđc(AB)}=\frac{1}{2}(x+10^0)=\frac{1}{2}(100^0+10^0)=55^0$
$\widehat{BAC}=180^0-\widehat{ABC}-\widehat{ACB}=180^0-65^0-55^0=60^0$
16 tháng 2 2023
góc COB=40+110=150 độ
=>sđ cung nhỏ BC=150 độ
sđ cung lớn BC=360-150=210 độ
CM
6 tháng 11 2018
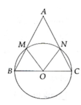
a, Chứng minh được ∆BOM = ∆CON (c.g.c) từ đó suy ra B M ⏜ = C N ⏜
b, Tính được M O N ^ = 100 0
NM
1
NB
2 tháng 5 2023
△ABC cân tại C
\(\Rightarrow\widehat{A}=\widehat{B}=\dfrac{180^o-\widehat{C}}{2}=\dfrac{180^o-40^o}{2}=70^o\)
A là góc nội tiếp chắn cung BC nhỏ
=> sdBC nhỏ = 2A= 2.70=140 độ