tìm x, y không âm thỏa mãn x - y = x2 +xy + y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 1 2020
Ta có x + y = 2 ⇒ y = 2 - x ≥ 0 ⇒ 0 ≤ x ≤ 2 . Thay y = 2 - x và biểu thức P ta được
P = 1 3 x 3 + x 2 + 2 - x 2 - x + 1 = 1 3 x 3 + 2 x 2 - 5 x + 5 = f x
với x ∈ 0 ; 2
Đạo hàm f ' x = x 2 + 4 x - 5 = 0 ⇔ x = 1 x = - 5
Do x ∈ 0 ; 2 nên loại x = -5
f 1 = 7 3 ; f 0 = 5 ; f 2 = 17 3
Vậy m i n x ∈ 0 ; 2 P = m i n x ∈ 0 ; 2 f x = 7 3 khi và chỉ khi x = 1
Đáp án B
TM
1
AH
Akai Haruma
Giáo viên
30 tháng 10 2023
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$P^2\leq (x+y)[(29x+3y)+(29y+3x)]=32(x+y)^2\leq 32.(x^2+y^2)(1+1)=64(x^2+y^2)\leq 64.2=128$
$\Rightarrow P\leq 8\sqrt{2}$
Vậy $P_{\max}=8\sqrt{2}$
NM
3
XO
25 tháng 7 2023
\(x^2+y^2+2\left(x+y\right)-xy=0\)
\(\Leftrightarrow4x^2-4xy+4y^2+8\left(x+y\right)=0\)
\(\Leftrightarrow\left(2x-y\right)^2+4\left(2x-y\right)+4+3y^2+12y+12=-16\)
\(\Leftrightarrow\left(2x-y+2\right)^2+3\left(y+2\right)^2=-16\)
Dễ thấy VT \(\ge0\) ; VP < 0 nên phương trình vô nghiệm
24 tháng 7 2023
\(x^2+y^2-2\left(x+y\right)=xy\)
\(\Rightarrow x^2-2x+1+y^2-2y+1=2+xy\)
\(\Rightarrow\left(x-1\right)^2+\left(y-1\right)^2=2+xy\)
Ta lại có : \(\left(x-1\right)^2+\left(y-1\right)^2\ge2\left(x-1\right)\left(y-1\right)\) (Bất đẳng thức Cauchy)
CM
29 tháng 4 2018
Chọn C.
Phương pháp:
Đưa biểu thức P về hàm số 1 ẩn x.
Khảo sát, tìm GTNN của hàm số đó.
Cách giải:
19 tháng 12 2020
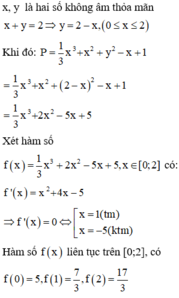
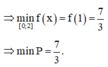
Ta có \(xy\le\dfrac{\left(x+y\right)^2}{4}\).
Do đó ta có: \(x+y+xy=x+y-2xy+3xy\le x+y-2xy+\dfrac{3}{4}\left(x+y\right)^2\)
\(\Rightarrow x^2+y^2\le x+y-2xy+\dfrac{3}{4}\left(x+y\right)^2\)
\(\Leftrightarrow\dfrac{1}{4}\left(x+y\right)^2-\left(x+y\right)\le0\)
\(\Leftrightarrow\left(x+y\right)\left[\dfrac{1}{4}\left(x+y\right)-1\right]\le0\)
\(\Leftrightarrow0\le x+y\le4\).
Do đó m = 0, n = 4.
Vậy m2 + n2 = 16. Chọn A.