cho tam giác cân ABC, có ACB =100 độ, phân giác góc A cắt BC tại D. CM: AD+BC=AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{BAC}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)
\(\Leftrightarrow\widehat{ABC}=\dfrac{180^0-100^0}{2}=40^0\)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy)
hay \(\widehat{ACB}=40^0\)
Vậy: \(\widehat{ABC}=40^0\); \(\widehat{ACB}=40^0\)

A B C H
Xét tam giác ABC vuông tại A
ta có AB2+AC2=BC2 (1)
Xét tam giác ABH vuông tại H
ta có BH2+AH2=AB2 (2)
Xét tam giác ACH vuông tại H
ta có CH2+AH2=AC2 (3)
Thay (2), (3) vào (1) ta có
BH2+AH2+CH2+AH2=BC2
BH2+2AH2+CH2=BC2

trên tia BC lấy M,N sao cho góc BDN=6O* , BDM=80*
CM được tam giáC BDN=BDA( g-c-g)
=> AD=DN , góc DNB=DAB=100*
=> DNC=80* = DMB
=> DN=DM =DA=MC(Tự chứng minh)
=>đpcm

a) Xét tam giác adb và tam giác acd có
góc b= góc c(giả thiết)(1)
Cạnh ad chung(2)
Góc bad=góc cad(3)
từ (1)và(3) => góc adb=acd(4)
từ (2) (3) (4) =>tam giác abd= tam giác acd(g-c-g)
=>ab=ad( 2 cạnh tương ứng)
b)Ta có adb=adc(cmt)
mà 2 góc này kề bù => adb=adc=180độ/2=90 độ
=>ad vuông góc với bc

Câu hỏi của •Ƙ - ƔℌŤ⁀ᶦᵈᵒᶫ - Toán lớp 7 - Học toán với OnlineMath

A B C I K
+) \(\Delta\)ABC cân => \(\hept{\begin{cases}AB=AC\left(1\right)\\\widehat{ABC}=\widehat{ACB}\end{cases}}\)
Ta có: \(\widehat{BAC}=100^o\)=> \(\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{BAC}}{2}=40^o\)
\(\widehat{IBC}=\widehat{ABC}-\widehat{ABI}=40^o-10^o=30^o\)
\(\widehat{ACI}=\widehat{BCI}=\frac{\widehat{ACB}}{2}=\frac{40^o}{2}=20^o\)(i)
+) Trên nửa mặt phẳng bờ AC chứa B lấy điểm K sao cho \(\Delta\)AKC đều => \(\hept{\begin{cases}\widehat{KAC}=\widehat{ACK}=\widehat{AKC}=60^o\\AK=KC=AC\left(2\right)\end{cases}}\)
=> \(\widehat{BAK}=\widehat{BAC}-\widehat{KAC}=100^o-60^o=40^o\)
Từ (1); (2) => AB=AK => \(\Delta\)ABK cân tại A => \(\widehat{ABK}=\widehat{AKB}=\frac{180^o-\widehat{BAK}}{2}=70^o\)
=> \(\widehat{KBC}=\widehat{ABK}-\widehat{ABC}=70^o-40^o=30^o\)
\(\widehat{KCB}=\widehat{KCA}-\widehat{ACB}=60^o-40^o=20^o\)
+) Xét \(\Delta\)BIC và \(\Delta\)BKC có:
\(\widehat{IBC}=\widehat{KBC}\left(=30^o\right)\)
BC chung
\(\widehat{ICB}=\widehat{KCB}\left(=20^o\right)\)
=> \(\Delta\)BIC = \(\Delta\)BKC
=> CK =CI (3)
(2); (3) => CI =CA => \(\Delta\)ACI cân tại C
b) \(\Delta\)ACI cân tại C có: \(\widehat{ACI}=20^o\) (theo (i) )
=> \(\widehat{CIA}=\widehat{CAI}=\frac{180^o-\widehat{ACI}}{2}=80^o\)
=> \(\widehat{BAI}=\widehat{BAC}-\widehat{CAI}=100^o-80^o=20^o\)

a: góc ABC+góc ACB=180-60=120 độ
=>góc IBC+góc ICB=60 độ
=>góc BIC=120 độ
b: góc BIE=góc DIC=60 độ
Xét ΔEBIvà ΔFBI có
BE=BF
góc EBI=góc FBI
BI chung
Do đo: ΔEBI=ΔFBI
=>góc EIB=góc FIB=60 độ
=>góc FIC=60 độ
=>góc FIC=góc DIC
Xét ΔFCI và ΔDCI có
góc FIC=góc DIC
IC chung
góc ICF=góc ICD
Do đó; ΔFCI=ΔDCI
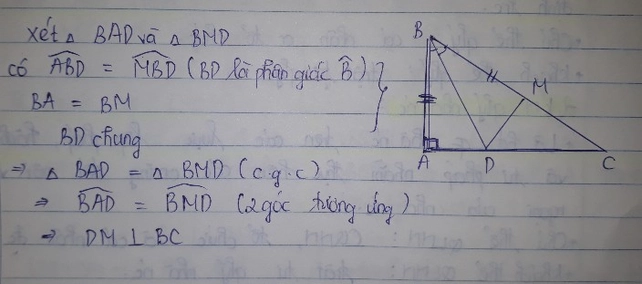 Đây là bài làm tương tự bạn tham khảo nhé!
Đây là bài làm tương tự bạn tham khảo nhé!