Mng giúp em với, em cảm ơn nhiều ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5

Câu 2:
uses crt;
var a:array[1..100]of integer;
i,n,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
t:=0;
for i:=1 to n do
if (4<a[i]) and (a[i]<15) then t:=t+a[i];
writeln(t);
readln;
end.


Bài 5:
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y-z}{2+3-4}=\dfrac{-20}{1}=-20\)
Do đó: x=-40; y=-60; z=-80

Bài 4:
a. ĐKXĐ: \(\left\{\begin{matrix} x-1\geq 0\\ x-1\neq 2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x\neq 3\end{matrix}\right.\)
b. \(B=\frac{x-3}{\frac{x-1-2}{\sqrt{x-1}+\sqrt{2}}}=\sqrt{x-1}+\sqrt{2}\)
\(x=4(2-\sqrt{3})\Rightarrow x-1=7-4\sqrt{3}=(2-\sqrt{3})^2\)
\(\Rightarrow \sqrt{x-1}=2-\sqrt{3}\Rightarrow B=\sqrt{x-1}+\sqrt{2}=2-\sqrt{3}+\sqrt{2}\)
c.
$\sqrt{x-1}\geq 0$ với mọi $x\geq 1; x\neq 3$
$\Rightarrow B=\sqrt{x-1}+\sqrt{2}\geq \sqrt{2}$
Vậy $B_{\min}=\sqrt{2}$ khi $x=1$
Bài 5:
\(C=\frac{x-2\sqrt{xy}+y+4\sqrt{xy}}{\sqrt{x}+\sqrt{y}}-\frac{\sqrt{xy}(\sqrt{x}-\sqrt{y})}{\sqrt{xy}}\)
\(=\frac{(\sqrt{x}+\sqrt{y})^2}{\sqrt{x}+\sqrt{y}}-(\sqrt{x}-\sqrt{y})=(\sqrt{x}+\sqrt{y})-(\sqrt{x}-\sqrt{y})\)
\(=2\sqrt{y}\) vẫn phụ thuộc vào biến $y$ bạn ạ. Bạn xem lại đề.

a: Thay x=2 và y=0 vào (d), ta được:
-n+3+4=0
=>1-n=0
hay n=1
b: Phương trình hoành độ giao điểm là:
\(x^2-2x+n-3=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot\left(n-3\right)=-4n+12+4=-4n+16\)
Để phương trình có hai nghiệm phân biệt thì -4n+16>0
hay n<4

 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
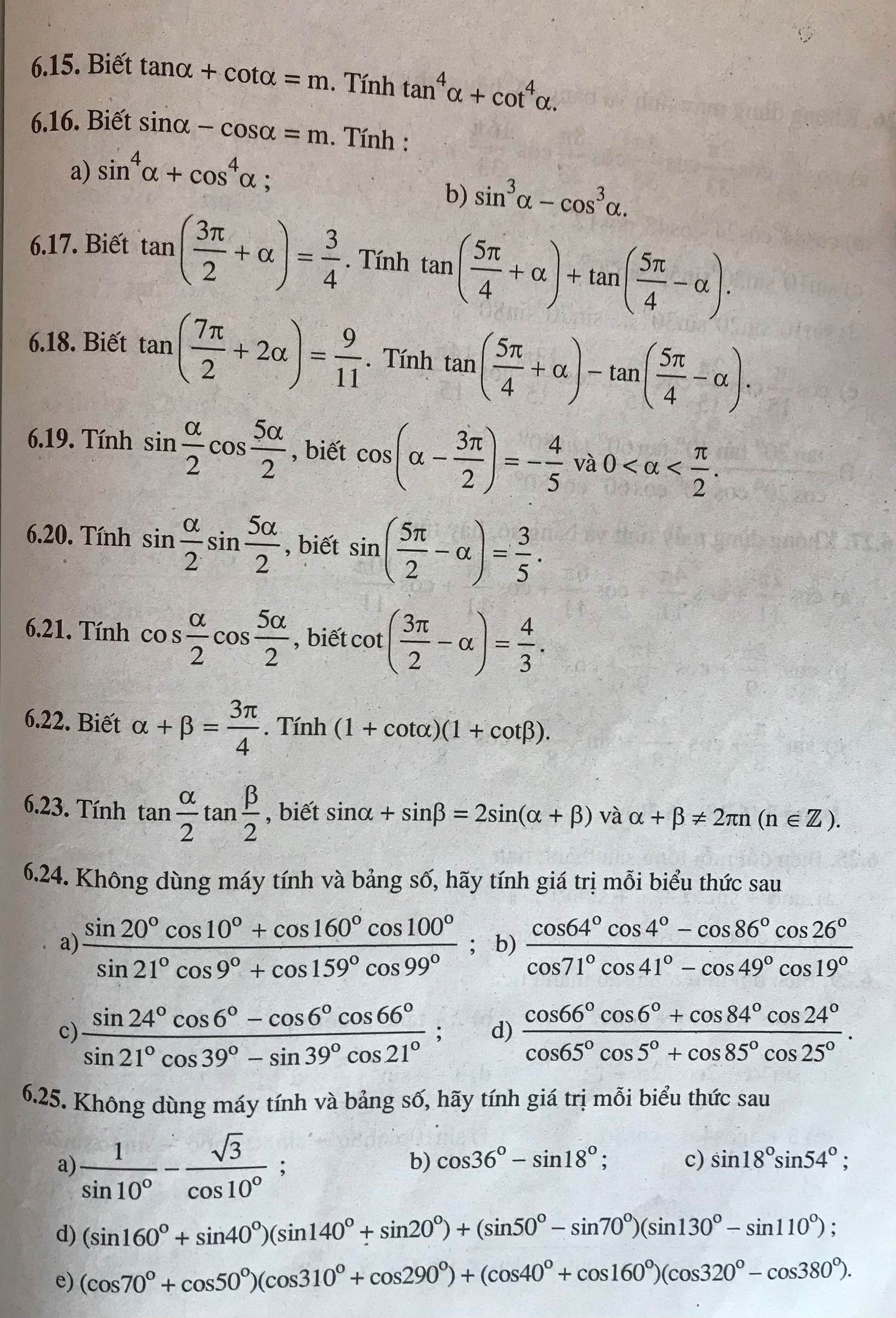
 mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33 



Câu 28: C
Câu 27: D
Câu 26: C
Câu 25: B