Giúp mình câu 2 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


is your pen blue or green
is your computer grey or black
i love football because it's interesting
i love guitar because very easy
you so funny
you so interesting
Or: Do you like to eat pizza or hamburgers?
Do you like red or yellow?
Because: I like elephants because they are friendly.
I don't go to school today because I'm sick.
So: I like to eat apples so much.
Thank you so much!


c, \(2H_2+O_2 \rightarrow2H_2O\)
\(n_{H_2}=\dfrac{33,6}{22,4}=1,5(mol) \Rightarrow n_{O_2}=0,75(mol)\)
\(V_{O_2}=22,4.0,75=16,8(l)\)
\(n_{H_2}=\dfrac{33,6}{22,4}=1,5\left(mol\right)\)
a. PTHH: \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
Theo PTHH: \(n_{Fe}=n_{H_2}=1,5\left(mol\right)\)
\(\Rightarrow m_{Fe}=56\cdot1,5=84\left(g\right)\)
b. Đổi: \(500ml=0,5l\)
\(CM_{H_2SO_4}=\dfrac{1,5}{0,5}=3M\)
c. \(2H_2+O_2\rightarrow2H_2O\)
Theo PTHH: \(n_{O_2}=\dfrac{1}{2}n_{H_2}=\dfrac{1}{2}\cdot1,5=0,75\left(mol\right)\)
\(\Rightarrow V_{O_2}=0,75\cdot22,4=16,8\left(l\right)\)

Câu 8 :
a) \(n_{Cu}=\dfrac{6,4}{64}=0,1\left(mol\right)\)
\(n_{Al}=\dfrac{54}{27}=2\left(mol\right)\)
b) \(V_{CO_2}=0,15.22,4=3,36\left(l\right)\)
\(V_{N_2}=0,3.22,4=6,72\left(l\right)\)
c) \(n_{hh}=n_{CO_2}+n_{H_2}=\dfrac{0,22}{44}+\dfrac{0,02}{2}=0,015\left(mol\right)\)
\(V_{hh}=0,015.22,4=0,336\left(l\right)\)
Câu 9
a) \(m_N=0,3.14=4.2\left(g\right)\)
\(m_{Cl}=0,4.35,5=14,2\left(g\right)\)
\(m_O=5.16=80\left(g\right)\)
b) \(m_{N_2}=0,2.28=5,6\left(h\right)\)
\(m_{Cl_2}=0,3.71=21,3\left(g\right)\)
\(m_{O_2}=4.32=128\left(g\right)\)
c) \(m_{Fe}=0,12.56=6,72\left(g\right)\)
\(m_{Cu}=3,15.64=201,6\left(g\right)\)
\(m_{H_2SO_4}=0,85.98=83,3\left(g\right)\)
\(m_{CuSO_4}=0,52.160=83,2\left(g\right)\)

Bài 1:
c, Xét tam giác BKC có:
BC < KB + KC (bất đẳng thức tam giác) (1)
mà BK = 2.KM, CK = 2.KN mà BK = CK, KM = KN (2)
Từ (1) và (2) suy ra BC < KB + KC = 4.KM
Vậy BC < 4.KM
Bài 2:
a, xét 2 tg vuông ABD và EBD có
góc A1 = góc E1
góc B1 = góc B2
BD cạnh chung
=> tg ABD= tg EBD
=> BA = BE
=> tg ABE cân
ta có trong tg cân đg phân giác hạ từ đỉnh xuống cạnh đối diện cũng là đg trug trực của tg
hay bd là đg trug trực của ae
b, xét 2 tg vuông ADF và EDC có
góc A2 = góc E2
AD = BE ( tg ABD = tg EBD )
góc D1 = góc D2 ( đối đỉnh )
=> tg ADF = tg EDC
=> DF = DC
c, ta có tg EDC có DC > DE ( ch > cgv )
mà AD = ED
=> AD < DC
d, ta có BA + AF = BF
BE + EC = BC
mà BA = BE
AF = EC ( tg ADF = tg EDF )
=> BF = BC
=> tg BFC cân
=> góc F = ( 180 độ - góc B ) /2 (1)
vì AB = EB => tam giác ABE cân
=> góc BAE = ( 180 độ - góc B ) /2 (2)
từ (1) và (2) => góc F = góc BAE
mà 2 góc này đồng vị
=> AE // FC

câu 2 phần 2:
\(\left\{{}\begin{matrix}4x+3y=11\\4x-y=7\end{matrix}\right.\)\(< =>\left\{{}\begin{matrix}4y=4\\4x-y=7\end{matrix}\right.< =>\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\).Vậy hệ pt có nghiệm
(x,y)=(2;1)
caau3 phần 2:
\(x^2-2x+m-1=0\)(1)
\(\Delta'=\left(-1\right)^2-\left(m-1\right)=1-m+1=2-m\)
để pt (1) có 2 nghiệm x1,x2<=>\(\Delta'\ge0< =>2-m\ge0< =>m\le2\)
theo vi ét=>\(\left\{{}\begin{matrix}x1+x2=2\left(1\right)\\x1.x2=m-1\left(3\right)\end{matrix}\right.\)
có: \(x1^4\)\(-x1^3=x2^4-x2^3\)
\(< =>x1^4-x2^4-x1^3+x2^3=0\)
\(< =>\left(x1^2-x2^2\right)\left(x1^2+x2^2\right)-\left(x1^3-x2^3\right)\)\(=0\)
\(< =>\left(x1-x2\right)\left(x1+x2\right)\left[\left(x1+x2\right)^2-2x1x2\right]\)\(-\left(x1-x2\right)\left(x1^2+x1x2+x^2\right)=0\)
\(< =>\)\(\left(x1-x2\right)\left[2.2^2-2\left(m-1\right)-\left(x1^2+x1x2+x2^2\right)\right]=0\)
\(< =>.\left(x1-x2\right)\left[8-2m+2-\left(x1+x2\right)^2+x1x2\right]=0\)
<=>\(\left(x1-x2\right)\left[10-2m-4+m-1\right]=0\)
\(< =>\left(x1-x2\right)\left(5-m\right)=0\)
\(=>\left[{}\begin{matrix}x1-x2=0\\5-m=0\end{matrix}\right.< =>\left[{}\begin{matrix}x1=x2\left(2\right)\\m=5\left(loai\right)\end{matrix}\right.\)
thế(2) vào(1)=>\(x1=x2=1\left(4\right)\)
thế (4) vào (3)=>\(m-1=1=>m=2\left(TM\right)\)
vậy m=2 thì....

 giúp mình câu 4 với câu 2 phần 2 với
giúp mình câu 4 với câu 2 phần 2 với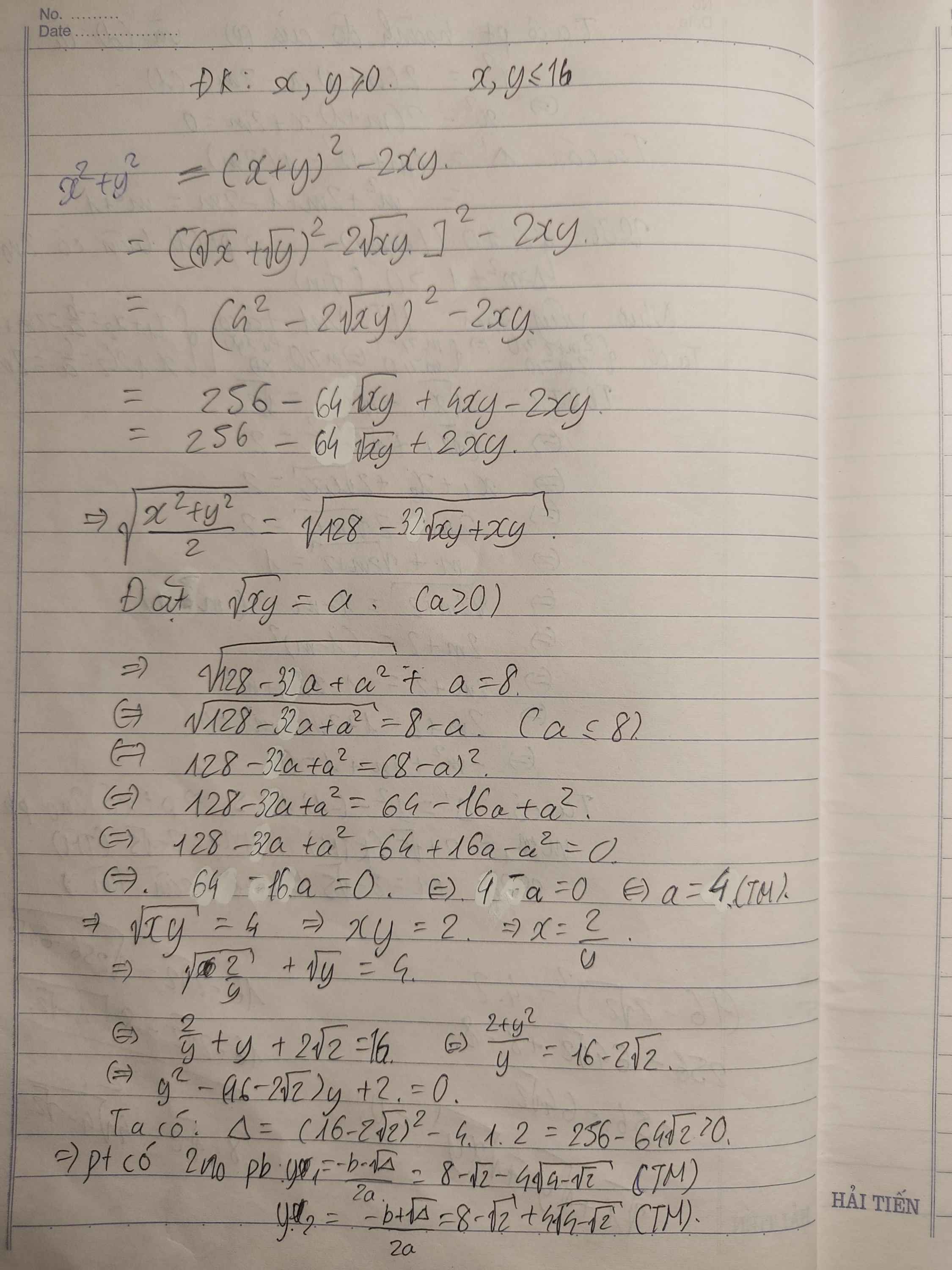
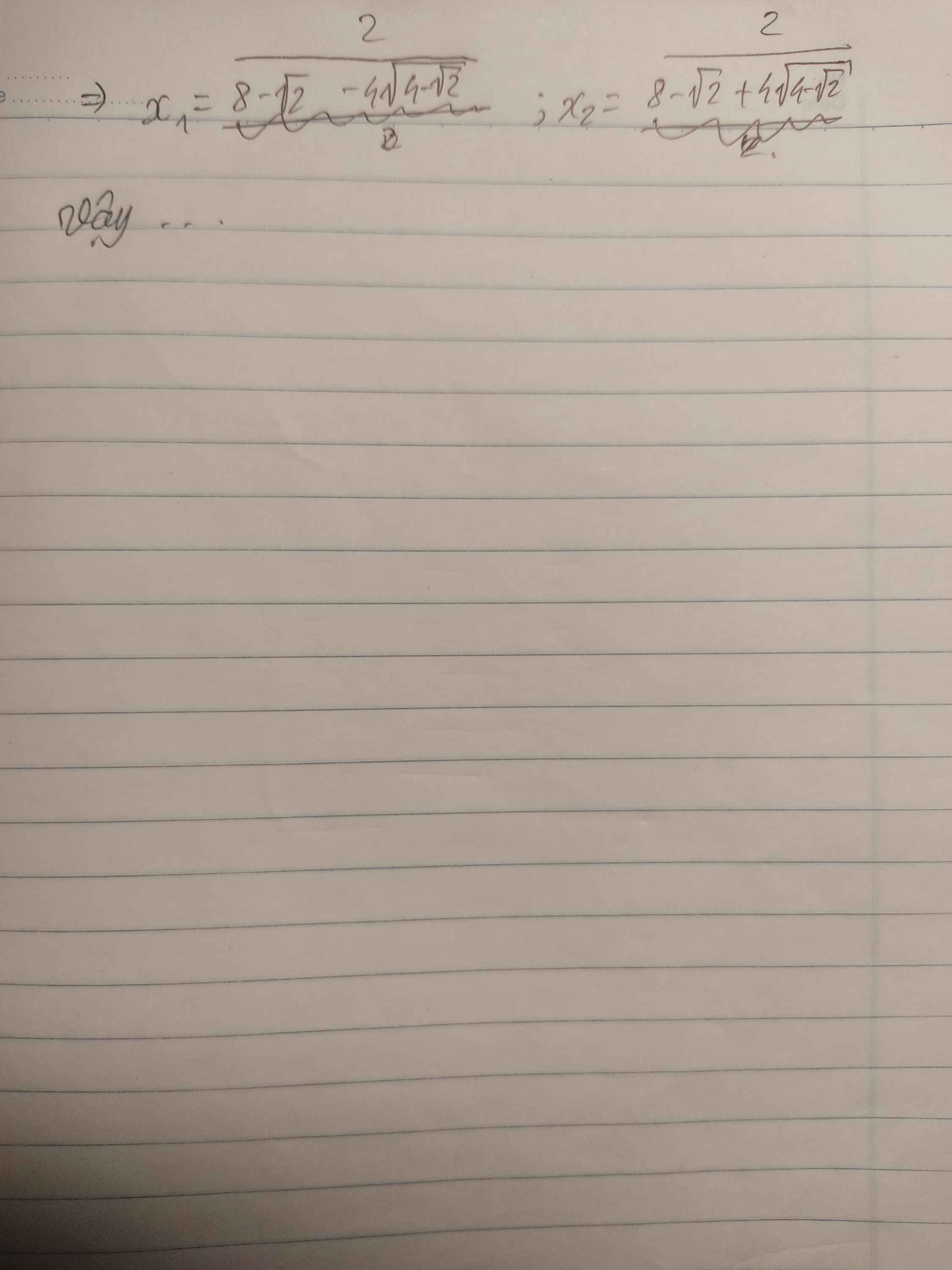
 Giúp mình câu 2 với câu 3 với , gấppppp!!!!!
Giúp mình câu 2 với câu 3 với , gấppppp!!!!! giúp mình câu c với ạ, 2 câu trên mình biết làm rồi
giúp mình câu c với ạ, 2 câu trên mình biết làm rồi giúp mình với mình chỉ cần 2 câu 8 với câu 9 thôi nha
giúp mình với mình chỉ cần 2 câu 8 với câu 9 thôi nha 
 giúp mình câu 1c và câu 2 với.
giúp mình câu 1c và câu 2 với.



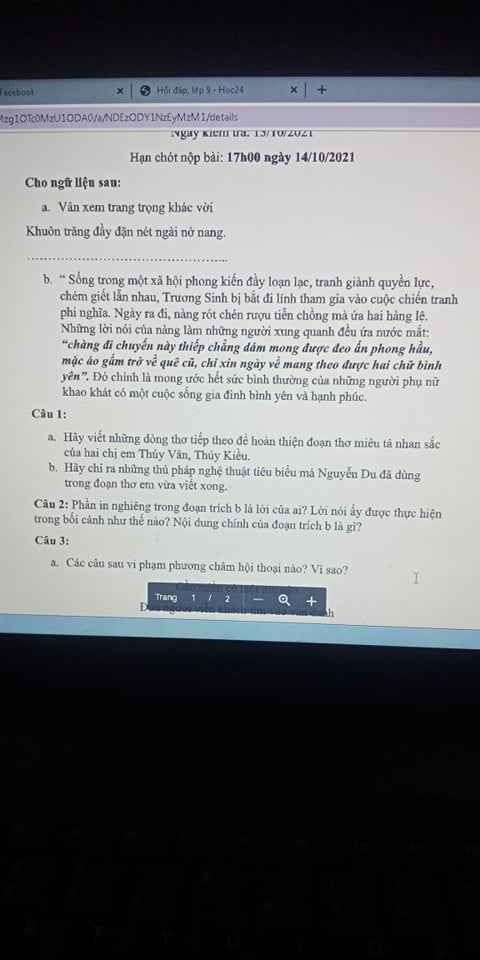 mọi người giúp mình bài này với câu 1 với câu 2 thôi
mọi người giúp mình bài này với câu 1 với câu 2 thôi
Bài 2:
a: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m-4\right)\left(m+3\right)\)
\(=4m^2-4m+1-4\left(m^2-m-12\right)\)
\(=4m^2-4m+1-4m^2+4m+48\)
=49>0
=>Phương trình luôn có hai nghiệm phân biệt
b: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m-4}\\x_1\cdot x_2=\dfrac{m+3}{m-4}\end{matrix}\right.\)
Theo đề, ta có:
\(\dfrac{4\left(m-1\right)^2}{\left(m-4\right)^2}-2\cdot\dfrac{m+3}{m-4}=9\)
\(\Leftrightarrow4\left(m-1\right)^2-2\left(m+3\right)\left(m-4\right)=9\left(m-4\right)^2\)
\(\Leftrightarrow4m^2-8m+4-2\left(m^2-m-12\right)=9\left(m^2-8m+16\right)\)
\(\Leftrightarrow4m^2-8m+4-2m^2+2m+24-9m^2+72m-144=0\)
\(\Leftrightarrow-7m^2+66m-116=0\)
\(\text{Δ}=66^2-4\cdot\left(-7\right)\cdot\left(-116\right)=1108\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-66-2\sqrt{277}}{-14}=\dfrac{33+\sqrt{55}}{7}\\x_2=\dfrac{33-\sqrt{55}}{7}\end{matrix}\right.\)
Để phương trình có 2 nghiệm phân biệt \(x_1;x_2.\)
\(\Rightarrow\) \(\Delta'>0.\Leftrightarrow\left(m-1\right)^2-\left(m-4\right)\left(m+3\right)>0.\)
\(\Leftrightarrow m^2-2m+1-m^2-3m+4m+12>0.\)
\(\Leftrightarrow-m+13>0.\Leftrightarrow m< 13.\)