Cho hàm số y = 3x - 2
a) Xác định các hệ số a, b. Tìm hai điểm thuộc đồ thị hàm số trên.
b) Tìm m để đường thẳng y = 3x - 2 cắt đường thẳngy = mx + 2.
cho mình xin lời giải chi tiết luôn nhaaaaa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương trình hoành độ giao điểm:
x
+
2
2
x
+
1
= mx + m - 1 ![]()
Để đường thẳng luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị thì phương trình (1) phải có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn ![]()
(1) có hai nghiệm phân biệt 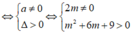
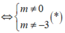
Theo định lý Vi – ét ta có 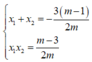
![]()
![]()
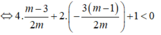
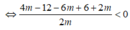
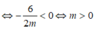

1.
Đồ thị hàm bậc 3 có 2 điểm cực trị nằm về 2 phía trục hoành khi và chỉ khi \(f\left(x\right)=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3+3x^2+mx+m-2=0\) có 3 nghiệm pb
\(\Leftrightarrow x^3+3x^2-2+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-2\right)+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+m-2=0\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}1-2+m-2\ne0\\\Delta'=1-\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow m< 3\)
2.
Pt hoành độ giao điểm:
\(\dfrac{2x-2}{x+1}=2x+m\)
\(\Rightarrow2x-2=\left(2x+m\right)\left(x+1\right)\)
\(\Leftrightarrow2x^2+mx+m+2=0\) (1)
d cắt (C) tại 2 điểm pb \(\Rightarrow\) (1) có 2 nghiệm pb
\(\Rightarrow\Delta=m^2-8\left(m+2\right)>0\Rightarrow\left[{}\begin{matrix}m>4+4\sqrt{2}\\m< 4-4\sqrt{2}\end{matrix}\right.\)
Khi đó, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-\dfrac{m}{2}\\x_Ax_B=\dfrac{m+2}{2}\end{matrix}\right.\)
\(y_A=2x_A+m\) ; \(y_B=2x_B+m\)
\(\Rightarrow AB^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2+\left(2x_A-2x_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2=1\)
\(\Leftrightarrow\left(x_A+x_B\right)^2-4x_Ax_B=1\)
\(\Leftrightarrow\left(-\dfrac{m}{2}\right)^2-4\left(\dfrac{m+2}{2}\right)=1\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10\\m=-2\end{matrix}\right.\)

Bài 10:
a: 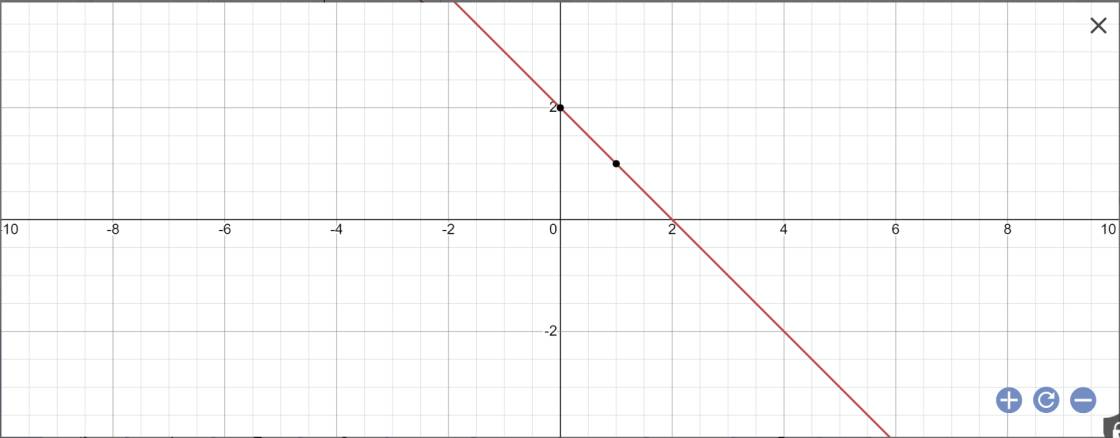
b:
y=-x+2
=>y+x-2=0
=>x+y-2=0
Khoảng cách từ O đến đến đường thẳng AB sẽ bằng khoảng cách từ O đến (d): y=-x+2
=>Khoảng cách từ O đến đường thẳng AB là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot1+0\cdot1+\left(-2\right)\right|}{\sqrt{1^2+1^2}}=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
Bài 9:
a: Vì hệ số góc của hàm số y=ax+b là 2 nên a=2
=>y=2x+b
Thay x=1 và y=-1 vào y=2x+b, ta được:
\(b+2\cdot1=-1\)
=>b+2=-1
=>b=-3
vậy: y=2x-3
b: Vì đồ thị của hàm số y=ax+b song song với đường thẳng y=-3x+2 nên \(\left\{{}\begin{matrix}a=-3\\b\ne2\end{matrix}\right.\)
Vậy: y=-3x+b
Thay x=0 và y=1 vào y=-3x+b, ta được:
\(b-3\cdot0=1\)
=>b-0=1
=>b=1
Vậy: y=-3x+1
Bài 9:
a. Hệ số góc của đths là $2$, tức $a=2$
ĐTHS đi qua điểm $A(1;-1)$ nên:
$-1=a.1+b$
$\Leftrightarrow -1=2.1+b\Rightarrow b=-3$
Vậy hàm số cần tìm là $y=2x-3$
b.
ĐTHS song song với $y=-3x+2$ nên $a=-3$
ĐTHS cần tìm cắt trục tung tại điểm có tung độ $1$, tức là nó đi qua điểm $(0;1)$
$\Rightarrow 1=a.0+b\Rightarrow b=1$
Vậy đths cần tìm là $y=-3x+1$

1. Đồ thị của hàm số đi qua điểm \(M\left(2;3\right)\) nên giá trị hoành độ và tung độ của \(M\) là nghiệm của phương trình đường thẳng trên, tức:
\(3=m\cdot2+m-6\Leftrightarrow m=3\left(TM\right)\)
2. Đồ thị hàm số song song với đường thẳng \(\left(d\right):y=3x+2\), khi: \(\left\{{}\begin{matrix}m=3\\m-6\ne2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne8\end{matrix}\right.\Rightarrow m=3\left(TM\right)\)
3. Gọi \(P\left(x_0;y_0\right)\) là điểm cố định mà đồ thị hàm số đi qua với mọi giá trị \(m\).
Khi đó: \(mx_0+m-6=y_0\Leftrightarrow\left(x_0+1\right)m-\left(y_0+6\right)=0\left(I\right)\)
Suy ra, phương trình \(\left(I\right)\) có vô số nghiệm, điều này xảy ra khi: \(\left\{{}\begin{matrix}x_0+1=0\\y_0+6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-1\\y_0=-6\end{matrix}\right.\).
Vậy: Điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị \(m\) là \(P\left(-1;-6\right)\).

b: f(-2)=-1/2*(-2)^2=-1/2*4=-2
=>M(-2;-2)
f(1)=-1/2*1^2=-1/2
=>N(1;-1/2)
Gọi (d): y=ax+b là phương trình đường thẳng cần tìm
Theo đề, ta có hệ: -2a+b=-2 và a+b=-1/2
=>a=1/2 và b=-1
=>y=1/2x-1
c: (D)//y=1/2x-1 nên (D): y=1/2x+b
PTHĐGĐ là:
-1/2x^2-1/2x-b=0
=>x^2+x+2b=0
Δ=1^2-4*1*2b=-8b+1
Để (P) cắt (D) tại một điểm duy nhất thì -8b+1=0
=>b=1/8
a)
a=3
b=-2
2 điểm C(1;1) và D (3;7)
b)
để 2 đường thẳng cắt nhau thì m khác 3