Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách từ ảnh đến thấu kính là:
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{d.f}{d-f}=\dfrac{8.4}{8-4}=8\left(cm\right)\)
Chiều cao của ảnh:
Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{8.2}{8}=2\left(cm\right)\)

\(k=\dfrac{d'}{d}=\dfrac{A'B'}{AB}=2\Rightarrow d'=2d\)
\(\dfrac{1}{d'}+\dfrac{1}{d}=\dfrac{1}{f}\Leftrightarrow\dfrac{1}{2d}+\dfrac{1}{d}=\dfrac{1}{12}\Rightarrow d=18\left(cm\right)\)

Ta có:
\(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{f}\)
\(\Rightarrow\dfrac{1}{16}+\dfrac{1}{d'}=\dfrac{1}{12}\)
\(\Rightarrow d'=48\)
Vậy khoảng cách từ ảnh đến thấu kính là 48cm

Nếu còn tiếp tục cop bài thiếu Tham Khảo từ hoidap247 nữa sẽ trực tiếp báo cáo lên admin box Lí khoá acc !!!

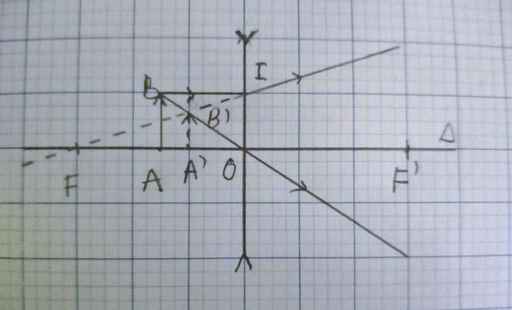
Tham khảo hình vẽ!!!
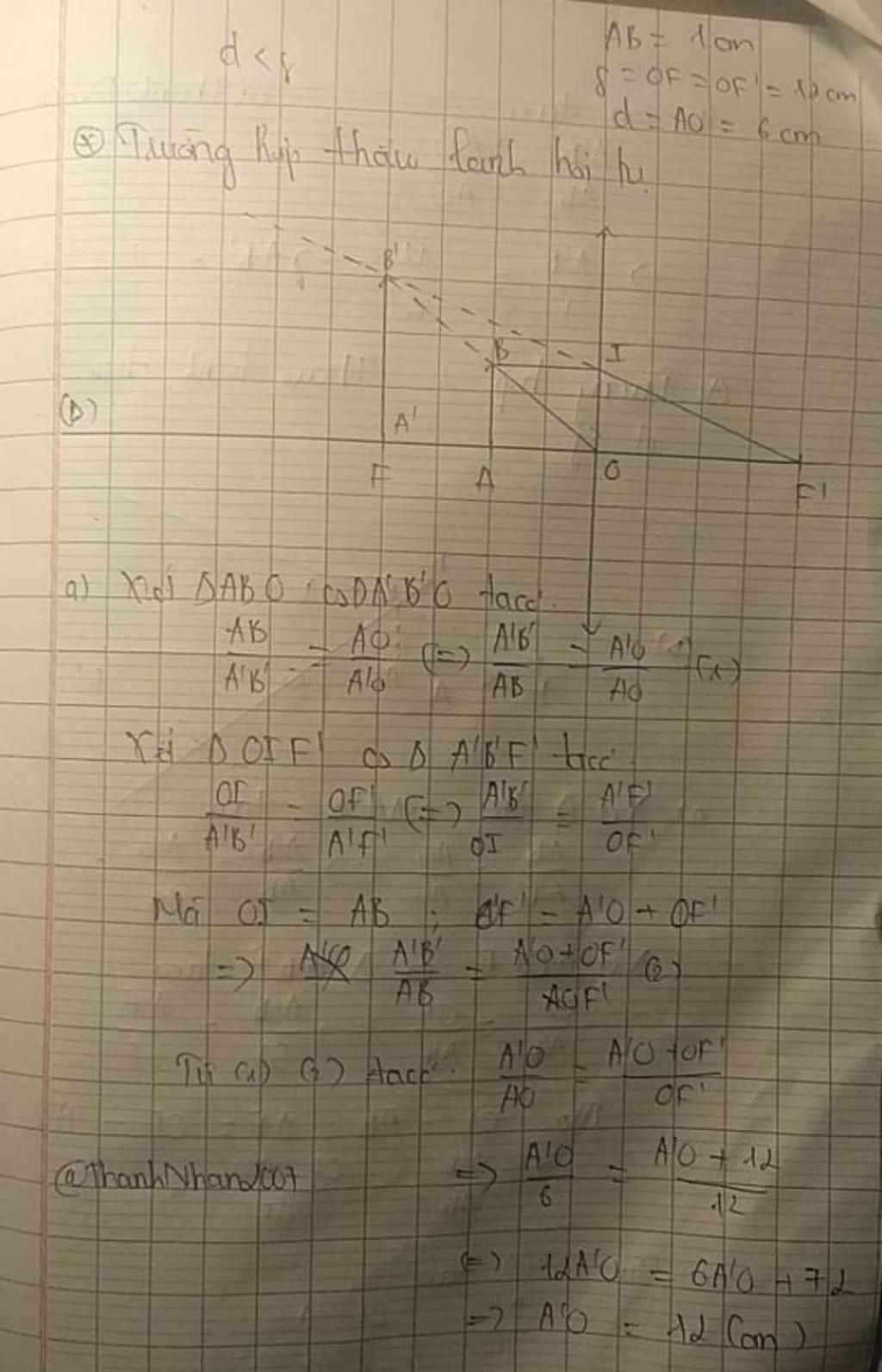
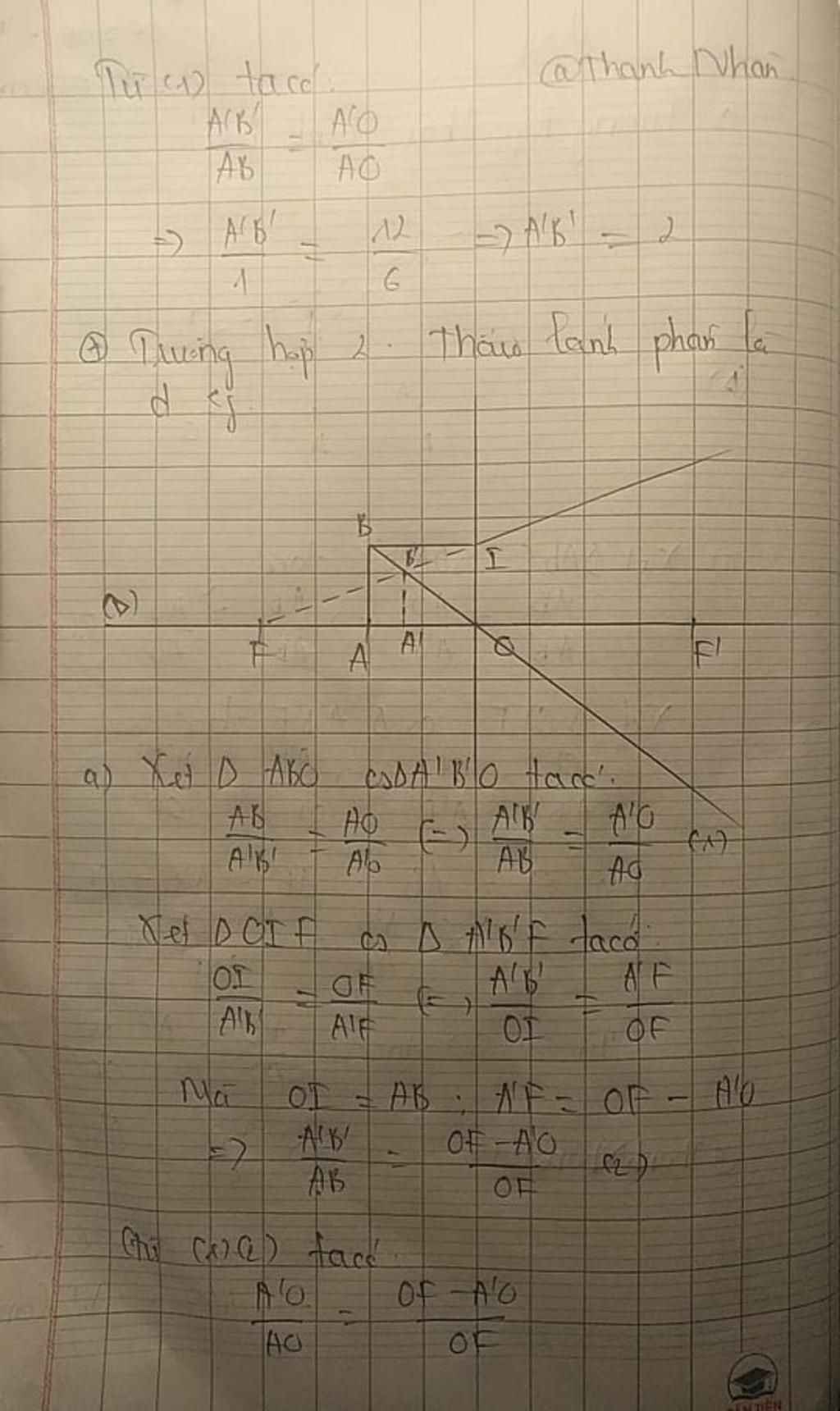
\(\Delta OAB\sim\Delta OA'B'\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\Rightarrow\dfrac{4}{A'B'}=\dfrac{4}{OA'}\left(1\right)\)
\(\Delta FA'B'\sim\Delta FOI\)
\(\Rightarrow\dfrac{OI}{A'B'}=\dfrac{OF}{OF-OA'}=\dfrac{OA}{A'B'}\)
\(\Rightarrow\dfrac{4}{A'B'}=\dfrac{12}{12-OA'}\left(2\right)\)
\(\Rightarrow\dfrac{4}{OA'}=\dfrac{12}{12-OA'}\Rightarrow OA'=3cm\)
\(\Rightarrow A'B'=\dfrac{AB\cdot OA'}{OA}=\dfrac{4\cdot3}{4}=3cm\)