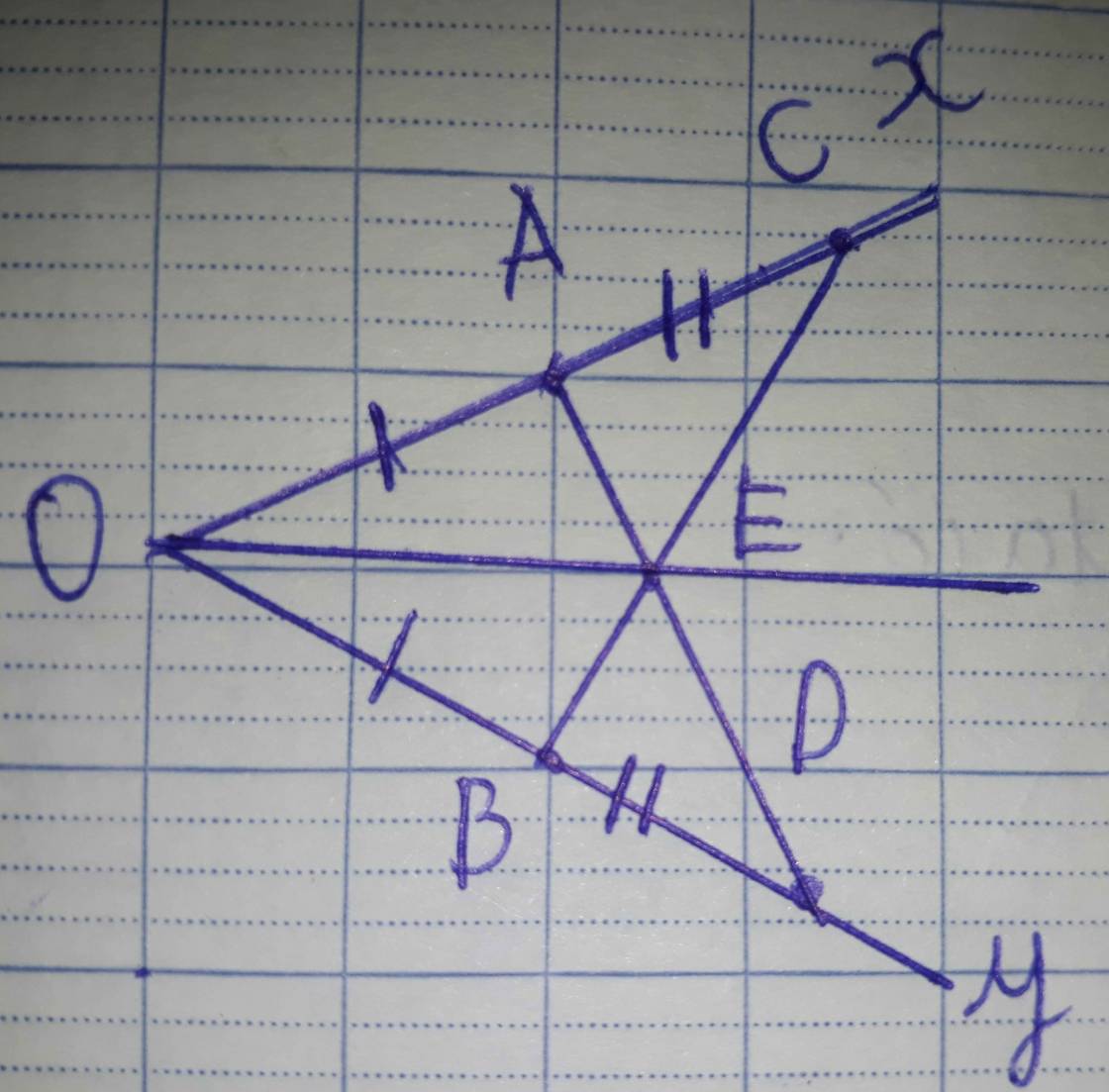
Cho góc nhọn zOy.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Trên tia Ax lấy điểm của AC và BD.
a,Chứng minh: góc ADN=BCN từ đó suy ra tam giác OAC = OBD?
b,Gọi N là giao điểm của AC và BD.Chứng minh tam giác ADN = BCN và ON là tia phân giác của góc xOy
c,Gọi H,K lần lượt là giao điểm của ON với DC và AB.Chứng minh OH vuông góc CD,AB // CD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Xét ΔBDC và ΔACD có
BD=AC
\(\widehat{BDC}=\widehat{ACD}\)
DC chung
Do đó: ΔBDC=ΔACD
Suy ra: \(\widehat{EAC}=\widehat{EBD}\)
Xét ΔEAC và ΔEBD có
\(\widehat{EAC}=\widehat{EBD}\)
AC=BD
\(\widehat{ECA}=\widehat{EDB}\)
Do đó: ΔEAC=ΔEBD
c: Xét ΔOEC và ΔOED có
OE chung
EC=ED
OC=OD
Do đó: ΔOEC=ΔOED
Suy ra: \(\widehat{COE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy

a: Xét ΔOAD và ΔOBC có
OA=OB
góc O chung
OD=OC
Do đó: ΔOAD=ΔOBC
=>AD=BC
b: Xét ΔEAC và ΔEBD có
góc EAC=góc EBD
AC=BD
góc ECA=góc EDB
Do đó: ΔEAC=ΔEBD

a, Xét △OBD vuông tại D và △OAC vuông tại C
Có: xOy là cạnh chung
OB = OA (gt)
=> △OBD = △OAC (ch-gn)
b, Vì △OBD = △OAC (cmt) => OD = OC (2 cạnh tương ứng) và OBD = OAC (2 góc tương ứng)
Ta có: OD + AD = OA và OC + CB = OB
Mà OA = OB (gt) ; OD = OC (cmt)
=> AD =BC
Xét △CIB vuông tại C và △DIA vuông tại D
Có: BC = AD (cmt)
CBI = DAI (2 góc tương ứng)
=> △CIB = △DIA (cgv-gnk)
=> IC = ID (2 cạnh tương ứng)
c, Xét △AOI và △BOI
Có: OA = OB (gt)
OI là cạnh chung
IA = IB (△DIA = △CIB)
=> △AOI = △BOI (c.c.c)
=> AOI = BOI (2 góc tương ứng)
=> OI là tia phân giác của góc AOB
hay OI là tia phân giác của góc xOy

a: Xét ΔOAC và ΔOBD có
OA=OB
\(\widehat{O}\) chung
OC=OD
Do đó: ΔOAC=ΔOBD
Suy ra: AC=BD
b: Xét ΔNBC và ΔNAD có
\(\widehat{NCB}=\widehat{NDA}\)
NB=NA
\(\widehat{CBN}=\widehat{DAN}\)
Do đó: ΔNBC=ΔNAD
Suy ra: NC=ND
Xét ΔOND và ΔONC có
ON chung
ND=NC
OD=OC
Do đó: ΔOND=ΔONC
Suy ra: \(\widehat{DON}=\widehat{CON}\)
hay ON là tia phân giác của góc xOy

a) xét ΔOCB và ΔODA, ta có :
OA = OB (giả thiết)
\(\widehat{O}\) là góc chung
AC = BD (giả thiết)
⇒ ΔOCB = ΔODA (c.g.c)
⇒ AC = BD (2 cạnh tương ứng)
b) xét ΔEAC và ΔEBD, ta có :
AD = BC (câu a)
\(\widehat{AEC}=\widehat{BED}\) (vì là 2 góc đối đỉnh)
AC = BD (giả thiết)
⇒ ΔEAC = ΔEBD (C.G.C)
c) xét ΔOAE và ΔOBE, ta có :
OA = OB (giả thiết)
AE = BE [vì ΔEAC = ΔEBD (2 cạnh tương ứng)]
OE là cạnh chung
⇒ ΔOAE = ΔOBE (c.c.c)
⇒ \(\widehat{AOE}=\widehat{BOE}\) (2 góc tương ứng)
Đề khó hiểu quá bạn