giúp mình bài 1 bài 2 dạng 1 vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 2:
a: Xét ΔBHA vuông tại H và ΔBHD vuông tại H có
BH chung
HA=HD
Do đó: ΔBHA=ΔBHD
b: Ta có: ΔBHA=ΔBHD
nên \(\widehat{ABH}=\widehat{DBH}\)
hay BH là tia phân giác của góc ABD

Mình có công thức tham khảo cho bạn đây:
Giả sử hợp chất AxBy:
Ta có: x . hóa trị A = y . hóa trị B
\(\Rightarrow \dfrac{x}{y}= \dfrac{hóa trị B}{hóa trị A}= \dfrac{b'}{a'}\). Chú ý: \(\dfrac{b'}{a'} \) là tỉ số tối giản nhé
\(\Rightarrow \begin{cases} x= hóa trị B=b'\\ y= hóa trị A= a'(2) \end{cases} \)
Ví dụ: Fe (III) và O:
Gọi CTHH là FexOy
Có: \(\dfrac{x}{y}= \dfrac{hóa trị O}{hóa trị Fe}= \dfrac{2}{3}\) \(\Rightarrow\)\(Fe_2O_3\)
Tương tự Cu và O
CTHH: Cu1O1 nhưng do chỉ số 1 không cần ghi nên CTHH là CuO
Tương tự bạn cũng có thể coi B trong AxBy là 1 nhóm như -(OH) ; =SO4;...
Cách 2) Bạn lấy Bội chung nhỏ nhất của hóa trị A và B trong AxBy.
x= BCNN : hóa trị A
y= BCNN : hóa trị B
Ví dụ: Al và O
Gọi CTHH là AlxOy
BCNN của hóa trị Al (III) và O(II) là 6
x= 6:3=2
y= 6:2 = 3
CTHH: Al2O3
Bạn đọc lại phần lập CTHH khi biết hóa trị nhé
C2) Theo thứ tự nhé:
\(P_2O_3 ; NH_3; FeO; Cu(OH)_2; Ca(NO_3)_2\)
\(Ag_2SO_4; Ba_3(PO_4)_2; Fe_2(SO_4)_3; Al_2(SO_4)_3; NH_4NO_3\)
C3) Theo thứ tự:
a) \(Na_2O\)
Ở CTHH trên, có 2 nguyên tử Na kết hợp với 1 nguyên tử O nên:
\(M_{Na_2O}= 2 . M_{Na} + 1. M_O=2 . 23 + 1 . 16=62 (g/mol)\)
b)
\(ZnCl_2; M_{ZnCl_2}=136 (g/mol)\)
c)\(Cu(OH)_2 \)
Ở đây, bạn thấy 1 nguyên tử Cu kết hợp với 2 nhóm OH nên ta có:
\(M_{Cu(OH)_2}= 1 . M_{Cu} + 2 . M_{nhóm -OH}= 1 . 64 + 2 . 17=98 (g/mol)\)
d)\(Fe(NO_3)_3; M_{Fe(NO_3)_3}=242 (g/mol)\)
e)\(AlPO_4; M= 122 (g/mol)\)
f)\(CaSO_4; M_{CaSO_4}= 136 (g/mol)\)

\(=2x^2\left(x-1\right)-4x\left(x-1\right)=\left(x-1\right)\left(2x^2-4x\right)=2x\left(x-2\right)\left(x-1\right)\)

Bài 1:
a: Ta có: \(5x^2-\left(2x+1\right)\left(x-2\right)-x\left(3x+3\right)+7\)
\(=5x^2-2x^2+4x-x+2-3x^2-3x+7\)
=9
b: Ta có: \(\left(3x-1\right)\left(2x+3\right)-\left(x-5\right)\left(6x-1\right)-38x\)
\(=6x^2+9x-2x-3-\left(6x^2-x-30x+5\right)-38x\)
\(=6x^2-31x-3-6x^2+31x-5\)
=-8

2. Sông Châu Giang làm cho cảnh sắc quê hương em thêm hữu tình, thơ mộng. Bốn mùa, dòng sông trong xanh, về mùa xuân, nước sông dâng đầy hơn, tỏng xanh hơn và hiền hòa hơn. Qua các dòng kênh tỏa khắp các cánh đồng, nước sông Châu Giang xanh màu xanh của lúa, cứ êm đềm trôi đi. Lúa xanh mơn mởn, mát mẻ, thanh bình. Ngắm dòng sông trôi mà lòng em lại lâng lâng lạ kì. Sông Châu Giang cung cấp nước cho cả một vùng quê lúa nước bao la, giúp cho cánh đồng xanh tươi quanh năm suốt tháng.
1. a) liệt kê không tăng tiến
b) liệt kê theo từng cặp
c) liệt kê không theo từng cặp

Lời giải:
ĐKXĐ: $x\neq \pm 3; x\neq 0$
a. \(A=\left[\frac{-(x-3)}{x+3}.\frac{(x+3)^2}{(x-3)(x+3)}+\frac{x}{x+3}\right].\frac{x+3}{3x^2}\)
\(=\left(-1+\frac{x}{x+3}\right).\frac{x+3}{3x^2}=\frac{-3}{x+3}.\frac{x+3}{3x^2}=\frac{-1}{x^2}\)
b. Với $x=\frac{-1}{2}$ thì $x^2=\frac{1}{4}$
$\Rightarrow A=\frac{-1}{\frac{1}{4}}=-4$
c.
Với $x\neq 0, \pm 3$ thì $\frac{1}{x^2}>0\Leftrightarrow A=\frac{-1}{x^2}< 0$ với mọi $x\neq 0; x\neq \pm 3$
a) Ta có: \(A=\left(\dfrac{3-x}{x+3}\cdot\dfrac{x^2+6x+9}{x^2-9}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
\(=\left(\dfrac{-\left(x-3\right)}{x+3}\cdot\dfrac{\left(x+3\right)^2}{\left(x+3\right)\left(x-3\right)}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
\(=\left(\dfrac{-x-3+x}{x+3}\right)\cdot\dfrac{x+3}{3x^2}\)
\(=-\dfrac{1}{x^2}\)

Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.




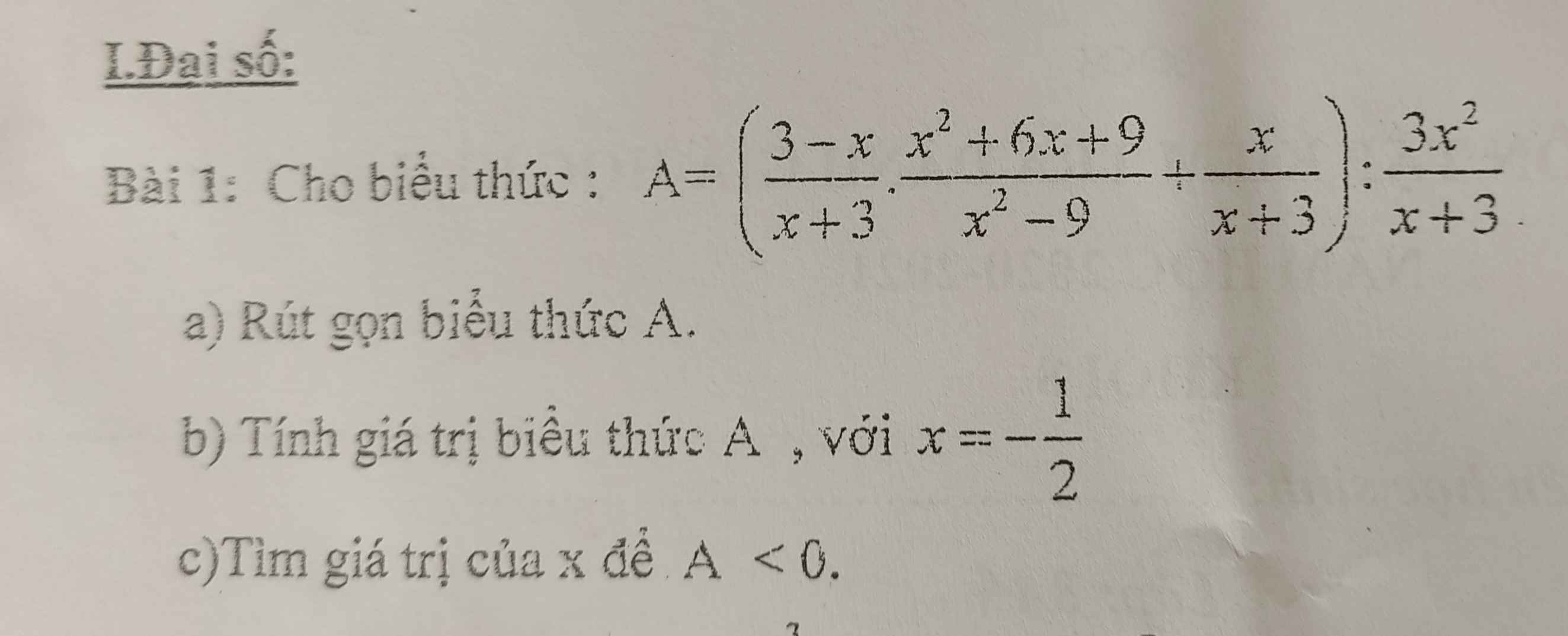
Bài 1:
a: \(=14x^3-7x^2+28x-14x^3=-7x^2+28x\)
b: \(=\dfrac{3x^3-6x^2+2x^2-4x-x+2}{x-2}=3x^2+2x-1\)
c: \(\Leftrightarrow\left(2x-3-5x\right)\left(2x-3+5x\right)=0\)
=>(-3x-3)(7x-3)=0
=>x=-1 hoặc x=3/7