Giúp em với mn ơi thứ6 em nộp rồi

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu c mình làm rồi: Mn ơi, hướng dẫn em cách để giống mẫu đi ạ! - Hoc24
\(d,\dfrac{x}{x^3-27}=\dfrac{x}{\left(x-3\right)\left(x^2+3x+9\right)}=\dfrac{x\left(x-3\right)}{\left(x-3\right)^2\left(x^2+3x+9\right)}\\ \dfrac{x+2}{x^2-6x+9}=\dfrac{x+2}{\left(x-3\right)^2}=\dfrac{\left(x+2\right)\left(x^2+3x+9\right)}{\left(x-3\right)^2\left(x^2+3x+9\right)}\\ \dfrac{x-1}{x^2+3x+9}=\dfrac{\left(x-1\right)\left(x-3\right)^2}{\left(x-3\right)^2\left(x^2+3x+9\right)}\)
\(f,\dfrac{x+2}{x^2-3x+2}=\dfrac{x+2}{\left(x-1\right)\left(x-2\right)}=\dfrac{\left(x+2\right)\left(2x-3\right)}{\left(x-1\right)\left(x-2\right)\left(2x-3\right)}\\ \dfrac{x}{-2x^2+5x-3}=\dfrac{-x}{\left(2x-3\right)\left(x-1\right)}=\dfrac{-x\left(x-2\right)}{\left(2x-3\right)\left(x-1\right)\left(x-2\right)}\\ \dfrac{2x+1}{-2x^2+7x-6}=\dfrac{-\left(2x+1\right)}{\left(x-2\right)\left(2x-3\right)}=\dfrac{-\left(2x+1\right)\left(x-1\right)}{\left(x-1\right)\left(x-2\right)\left(2x-3\right)}\)
\(\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{\left(a+x\right)}{\left(2x+a\right)\left(3x-2a\right)}\)
\(\dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{a-x}{\left(x+2a\right)\left(3x-2a\right)}\)
Do đó ta quy đồng:
\(\dfrac{a+x}{6x^2-ax-2a^2}=\dfrac{\left(a+x\right)\left(x+2a\right)}{\left(x+2a\right)\left(2x+a\right)\left(3x-2a\right)}\)
\(\dfrac{a-x}{3x^2+4ax-4a^2}=\dfrac{\left(a-x\right)\left(2x+a\right)}{\left(x+2a\right)\left(2x+a\right)\left(3x-2a\right)}\)



b, \(cos^25x-sin^2x=0\)
\(\Leftrightarrow cos^25x-cos^2\left(x-\dfrac{\pi}{2}\right)=0\)
\(\Leftrightarrow\left[cos5x-cos\left(x-\dfrac{\pi}{2}\right)\right]\left[cos5x+cos\left(x-\dfrac{\pi}{2}\right)\right]=0\)
\(\Leftrightarrow-4sin\left(3x-\dfrac{\pi}{4}\right).sin\left(2x+\dfrac{\pi}{4}\right).cos\left(3x-\dfrac{\pi}{4}\right).cos\left(2x+\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow-sin\left(6x-\dfrac{\pi}{2}\right).sin\left(4x+\dfrac{\pi}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(6x-\dfrac{\pi}{2}\right)=0\\sin\left(4x+\dfrac{\pi}{2}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}6x-\dfrac{\pi}{2}=k\pi\\4x+\dfrac{\pi}{2}=k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+\dfrac{k\pi}{6}\\x=-\dfrac{\pi}{8}+\dfrac{k\pi}{4}\end{matrix}\right.\)








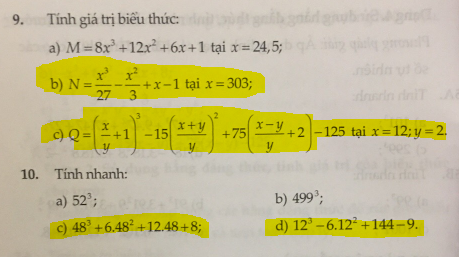 Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người.
Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người. 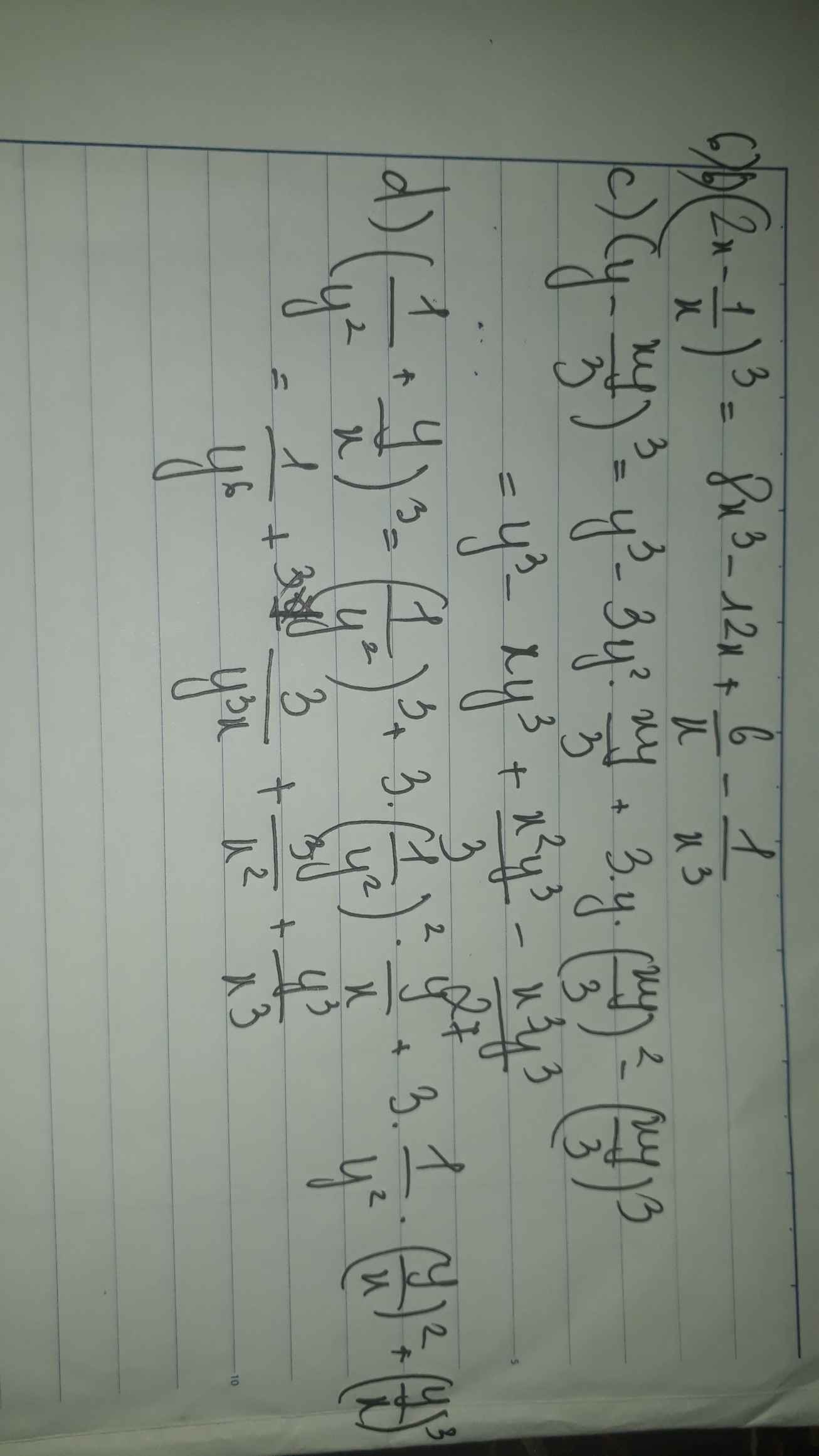
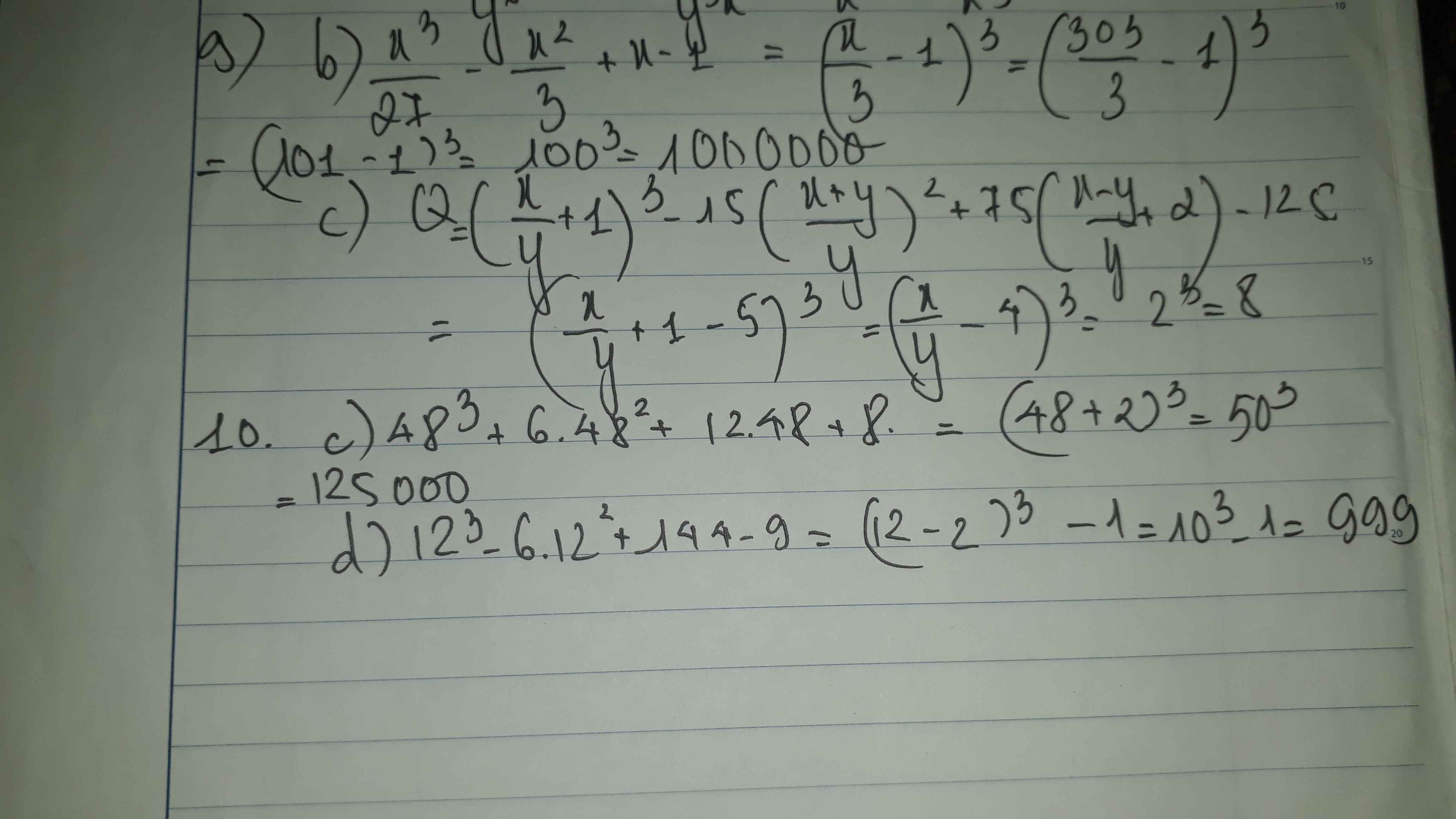
giúp gì , có cái gì đâu mà giúp