Tam giác ABC cân ở A có M là trung điểm BC, H là hình chiếu của M xuống AC, O là trung điểm của MH. C/m OA vuông góc với BH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

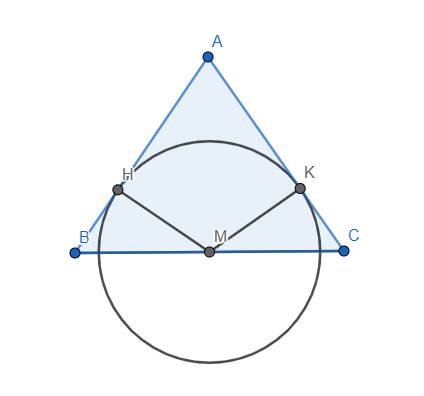
Gọi K là hình chiếu của M lên AC. Xét tam giác MBH vuông tại H và MCK vuông tại K, ta có:
\(MB=MC\) (M là trung điểm BC); \(\widehat{B}=\widehat{C}\) (tam giác ABC cân tại A)
\(\Rightarrow\Delta MBH=\Delta MCK\left(ch-gn\right)\) \(\Rightarrow MH=MK\)
Ta thấy MK chính là khoảng cách từ AC đến M, đồng thời MK bằng MH là bán kính của đường tròn (M; MH) nên AC tiếp xúc với (M) (đpcm)

\(a,\left\{{}\begin{matrix}BM=MC\\MH//AC\left(\perp AB\right)\end{matrix}\right.\Rightarrow AH=HB\) hay H là trung điểm AB
\(b,\left\{{}\begin{matrix}BM=MC\\AH=HB\end{matrix}\right.\Rightarrow MH\) là đtb tg ABC
\(\Rightarrow MH=\dfrac{1}{2}AC\)
Mà \(AC^2=BC^2-AB^2=144\left(pytago\right)\Rightarrow AC=12\left(cm\right)\)
\(\Rightarrow MH=6\left(cm\right)\)

a/
\(BN\perp AC;MH\perp AC\) => MH//BN
Xét tg BNC có
MH//BN
MB=MC
=> HN=HC (trong tg đường thẳng // với 1 cạnh và đi qua trung điểm của 1 cạnh thì đi qua trung điểm cạnh còn lại)
Ta có
MH//BN. Xét tg AMH
\(\dfrac{ED}{IM}=\dfrac{EN}{IH}\) (talet)
Mà IM=IH => ED=EN
b/
Xét tg vuông ABN có
\(BN^2=AB^2-AN^2=AC^2-AN^2=\)
\(=AC^2-\left(AC-CN\right)^2=AC^2-\left(AC-2HN\right)^2=\)
\(=AC^2-AC^2+4AC.HN-4HN^2=\)
\(=4HN.\left(AC-HN\right)=4HN\left(AC-HC\right)=\)
\(=4HN.HA\)
Xét tg BCN có
MB=MC; HN=HC => MH là đường trung bình => \(MH=\dfrac{BN}{2}\)
Mà MH=2MI\(\Rightarrow2MI=\dfrac{BN}{2}\Rightarrow BN=4MI\)
Ta có
\(BN^2=4HN.HA\Rightarrow\left(4MI\right)^2=4HN.HA\)
\(\Rightarrow16MI^2=4.HN.HA\Rightarrow MI^2=HN.HA\)