Giúp mình với đi ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


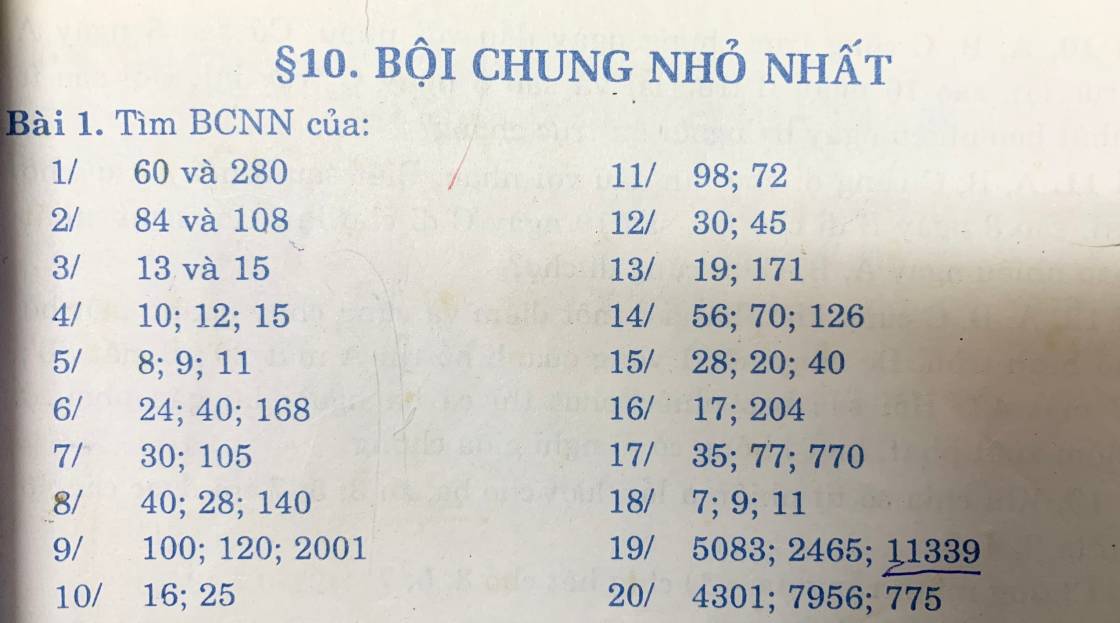
1: 60=2^2*3*5
280=2^3*5*7
=>BCNN(60;280)=2^3*5*7*3=840
2: 84=2^2*3*7
108=2^2*3^3
=>BCNN(84;108)=2^2*3^3*7=756
3: 13=13
15=3*5
=>BCNN(13;15)=13*3*5=195
4: 10=2*5
12=2^2*3
15=3*5
=>BCNN(10;12;15)=2^2*3*5=60
5: 8=2^3; 9=3^2; 11=11
=>BCNN(8;9;11)=2^3*3^2*11=72*11=792
6: 24=2^3*3
40=2^3*5
168=2^3*3*7
=>BCNN(24;40;168)=2^3*3*5*7=840
7: 30=2*3*5
105=3*5*7
=>BCNN(30;105)=2*3*5*7=210
8: 40=2^3*5
28=2^2*7
140=2^2*5*7
=>BCNN(40;28;140)=2^3*5*7=240
10: 16=2^4
25=5^2
=>BCNN(16;25)=2^4*5^2=400


\(\dfrac{1}{2}sin6x\ne0\)\(\Leftrightarrow sin6x\ne0\) \(\Leftrightarrow6x\ne k\pi\)\(\Leftrightarrow x\ne\dfrac{k\pi}{6}\)
\(\dfrac{1}{2}\ne0\) rồi nên chỉ cần \(sin6x\ne0\)


2:
a: Xét tứ giác OAMD có
\(\widehat{OAM}+\widehat{ODM}=90^0+90^0=180^0\)
=>OAMD là tứ giác nội tiếp
b: Xét (O) có
ΔADC nội tiếp
AC là đường kính
Do đó: ΔADC vuông tại D
=>AD\(\perp\)BC tại D
Xét ΔABC vuông tại A có AD là đường cao
nên \(AD^2=DB\cdot DC\)
Xét (O) có
MA,MD là tiếp tuyến
Do đó: MA=MD
=>\(\widehat{MAD}=\widehat{MDA}\)
mà \(\widehat{MAD}+\widehat{MBD}=90^0\)(ΔADB vuông tại D)
và \(\widehat{MDA}+\widehat{MDB}=\widehat{BDA}=90^0\)
nên \(\widehat{MDB}=\widehat{MBD}\)
=>MD=MB
mà MD=MA
nên MB=MA
=>M là trung điểm của AB
Xét ΔABC có
M,O lần lượt là trung điểm của AB,AC
=>MO là đường trung bình
=>MO//BC

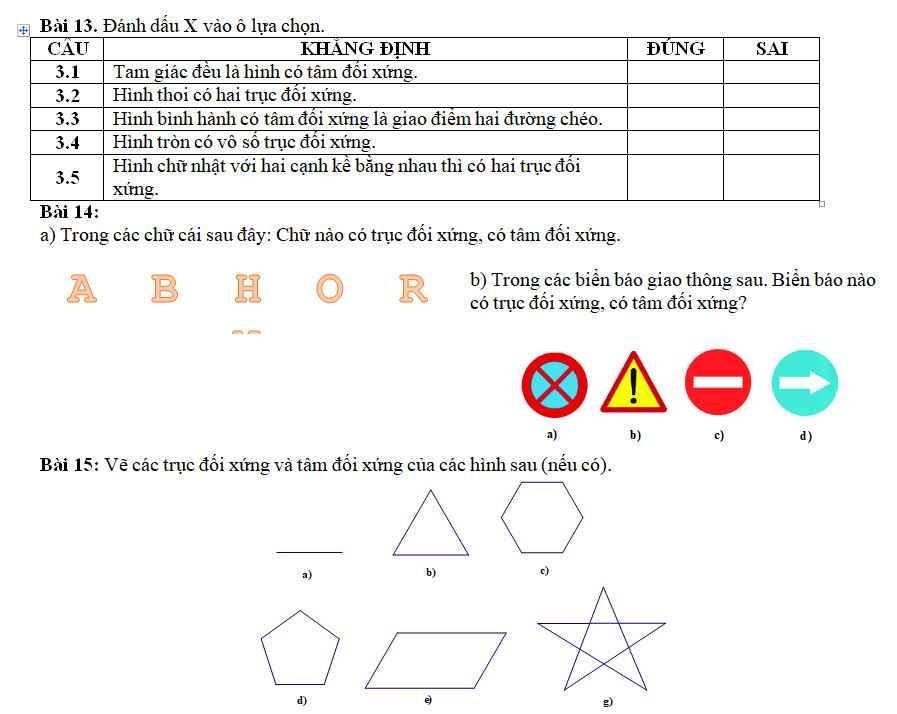 giúp mình bài 15 với đi ạ mình đng cần gấp
giúp mình bài 15 với đi ạ mình đng cần gấp
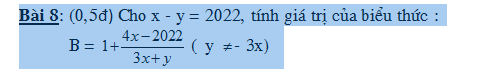 mọi người giúp mình với ạ, mai mình đi thi thi. Cảm ơn mọi người nhiều
mọi người giúp mình với ạ, mai mình đi thi thi. Cảm ơn mọi người nhiều 
