A=1/3 + 1/6 + 1/12 +1/24 + ............+ 1/768 + 1/1536
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 7 2023
\(A=\dfrac{1}{3}\left(1+\dfrac{1}{2}+...+\dfrac{1}{256}+\dfrac{1}{512}\right)\)
Đặt B=1+1/2+...+1/256+1/512
=>2B=2+1+...+1/128+1/256
=>B=2-1/512=1023/512
=>\(A=\dfrac{1}{3}\cdot\dfrac{1023}{512}=\dfrac{341}{512}\)
VN
4
29 tháng 4 2019
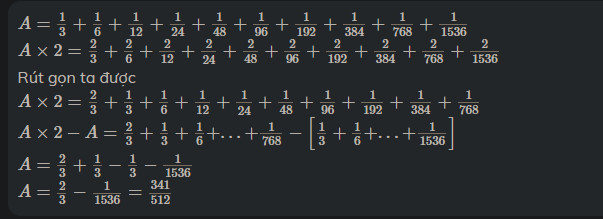
\(A=\frac{1}{3}+\frac{1}{6}+\frac{1}{12}+\frac{1}{24}+\frac{1}{48}+\frac{1}{96}+\frac{1}{192}+\frac{1}{384}+\frac{1}{768}+\frac{1}{1536}\)
\(A\times2=\frac{2}{3}+\frac{2}{6}+\frac{2}{12}+\frac{2}{24}+\frac{2}{48}+\frac{2}{96}+\frac{2}{192}+\frac{2}{384}+\frac{2}{768}+\frac{2}{1536}\)
Rút gọn ta được
\(A\times2=\frac{2}{3}+\frac{1}{3}+\frac{1}{6}+\frac{1}{12}+\frac{1}{24}+\frac{1}{48}+\frac{1}{96}+\frac{1}{192}+\frac{1}{384}+\frac{1}{768}\)
\(A\times2-A=\frac{2}{3}+\frac{1}{3}+\frac{1}{6}+...+\frac{1}{768}-\left[\frac{1}{3}+\frac{1}{6}+...+\frac{1}{1536}\right]\)
\(A=\frac{2}{3}+\frac{1}{3}-\frac{1}{3}-\frac{1}{1536}\)
\(A=\frac{2}{3}-\frac{1}{1536}=\frac{341}{512}\)
OK
0
DT
2
15 tháng 3 2016
Gọi tổng đó là A
A = 1/6+1/12+1/24+...+1/768
A x 2 = 1/3 + 1/6 + 1/12 + 1/24 + .... + 1/384
A x 2 - A = 1/3 + 1/6 + 1/12 + 1/24 + .... + 1/384 - 1/6 + 1/12 + 1/24 + ... + 1/768
A = 1/3 - 1/768 = 85/256