tam giác abc có ab>ac. trên ab,ac lấy n, sao cho an=am. gọi o là giao của bm và cn. chứng minh ob>oc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 10 2021
Do AB>AC nên lấy điểm P trên AB sao cho AP=AC . GỌi D là giao điểm của CN zà PM . DO AN =AM<AC=AP nên P nằm giữa N zà B nha
từ đó ˆBMN>ˆPMN
tự CM tam giác DMN cân tại D ( dễ tự làm ) nên ˆPMN=ˆCNM⇒ˆBMN>ˆCNM⇒ˆOMN>ˆONM
trong tam giác OMN có ˆOMN>ˆONM=>ON>OM(1)
tự xét tam giác APM = tam giác CAN (c,g.c nha)
=> PM=CN
doΔAPCcân tại A nên ˆAPC<900=>ˆAPM<900hayˆBPM>900
trong tam giác PBM có góc BPM > 90 độ mà lại là góc lớn nhất nên BM>PM=CN(2)
từ 1 zà 2 suy ra BM-OM>CN-ON hay OB>OC
KS
1 tháng 3 2018
Áp dụng định lí Mê-nê-la-uýt trong tam giác ABN ta có:
MA/MB.OB/ON.CN/CA=1
3/1.OB/ON.1,5/4,5=1
⇒OB/ON=1
Áp dụng định lí Mê-nê-la-uýt trong tam giác ACM ta có:
NA/NC.OC/OM.BM/BA=1
3/1,5.OC/OM.1/4=1
OC/OM=2
Vậy OB/ON+OC/OM=3
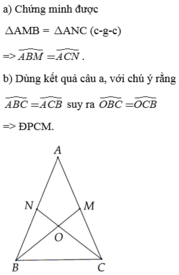
mk ghét nhất là lm bài hình về tam giác đẫ thế vt giả thiết kết luận tốn thì giờ
bài này thì cần gì viết gt, kl