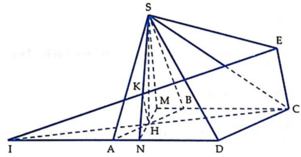
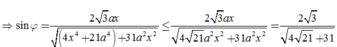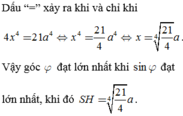Cho hình thoi ABCD có góc BAD bằng 500, O là giao điểm của AC và BD, H là hình chiếu của điểm O trên AB. Trên tia đối của BC lấy M, trên tia đối của DC lấy N sao cho HM //AN. Tính số đo góc MON.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 1 2022
\(\Delta ADB\text{ cân tại A}\Rightarrow\widehat{ADB}=\dfrac{180^0-\widehat{BAD}}{2}=65^0\\ \text{Ta có }\widehat{MBH}=\widehat{BCD}=\widehat{ADN}=\widehat{BAD}=50^0\\ \Rightarrow\widehat{ODN}=\widehat{ADB}+\widehat{ADN}=115^0\\ MH\text{//}AN\Rightarrow\widehat{MHA}=\widehat{HAN}\\ \Rightarrow\widehat{MHB}+\widehat{MBH}=\widehat{BAD}+\widehat{NAD}\\ \Rightarrow\widehat{MHB}=\widehat{NAD}\\ \Rightarrow\Delta MHB\sim\Delta AND\left(g.g\right)\\ \Rightarrow\dfrac{MB}{AD}=\dfrac{HB}{ND}\Rightarrow MB\cdot NC=AD\cdot HB\left(1\right)\)
\(\left\{{}\begin{matrix}\widehat{OHB}=\widehat{AOD}=90^0\\\widehat{HBO}=\widehat{ODA}\end{matrix}\right.\Rightarrow\Delta HBO\sim\Delta ODA\\ \Rightarrow\dfrac{HB}{OD}=\dfrac{OB}{AD}\Rightarrow HB\cdot AD=OB\cdot OD\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow\dfrac{MB}{OD}=\dfrac{OB}{ND}\\ \text{Mà }\widehat{MBO}=\widehat{NDO}\\ \Rightarrow\Delta MBO\sim\Delta ODN\left(c.g.c\right)\\ \Rightarrow\widehat{MOB}=\widehat{OND}\Rightarrow\widehat{MOB}+\widehat{NOD}=\widehat{OND}+\widehat{NOD}\\ \Rightarrow\widehat{MOB}+\widehat{NOD}=180^0-\widehat{NDO}=65^0\\ \Rightarrow180^0-\widehat{MON}=65^0\\ \Rightarrow\widehat{MON}=115^0\)
CM
29 tháng 1 2018
Đáp án A
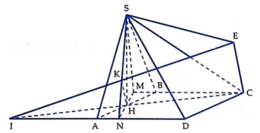
Gọi φ là góc giữa SC và (SAD), N là giao điểm của HM và AD, K là hình chiếu vuông góc của H trên SN, I là giao điểm của HC với AD. Gọi E là điểm đối xứng với I qua K.
Ta có M B = 1 4 B C = a 2 , H B = a , H B M ^ = B A D ^ = 60 °
⇒ H M = H B 2 + M B 2 − 2 H B . M B . c o s H B M ^
⇒ H M = a 2 + a 2 4 − 2 a . a 2 . cos 60 ° = 3 2 a
⇒ H M 2 + M B 2 = 3 2 a 2 + a 2 2 = a 2 = H B 2
⇒ Δ H M B vuông tại M
⇒ H M ⊥ M B hay M N ⊥ B C .
Vì S H ⊥ A D do S H ⊥ A B C D M N ⊥ A D do M N ⊥ B C ⇒ A D ⊥ S M N ⇒ A D ⊥ H K , mà H K ⊥ S N nên H K ⊥ S A D . Lại có HK là đường trung bình của Δ I C E nên H K // C E . Suy ra C E ⊥ S A D tại E và SE là hình chiếu của SC trên mặt phẳng (SAD).
Vậy φ = S C , S A D ^ = S C , S E ^ = C S E ^ .
Đặt S H = x , x > 0 . Do Δ S H N vuông tại H có HK là đường cao nên ta có
1 H K 2 = 1 S H 2 + 1 H N 2 ⇒ H K = S H . H N S H 2 + H N 2 = 3 a x 4 x 2 + 3 a 2 ⇒ C E = 2 H K = 2 3 a x 4 x 2 + 3 a 2
Do Δ S H C vuông tại H nên
S C = S H 2 + H C 2 = S H 2 + H M 2 + M C 2 = x 2 + 3 2 a 2 + 5 a 2 2 = x 2 + 7 a 2
Δ S E C vuông tại E nên sin φ = sin C S E ^ = E C S C = 2 3 a x 4 x 2 + 3 a 2 x 2 + 7 a 2
⇒ sin φ = 2 3 a x 4 x 4 + 21 a 4 + 31 a 2 x 2 ≤ 2 3 a x 4 21 a 2 x 2 + 31 a 2 x 2 = 2 3 4 21 + 31
Dấu “=” xảy ra khi và chỉ khi 4 x 4 = 21 a 4 ⇔ x 4 = 21 4 a 4 ⇔ x = 21 4 4 a .
Vậy góc φ đạt lớn nhất khi sin φ đạt lớn nhất, khi đó S H = 21 4 4 a
29 tháng 8 2023
a:
ABCD là hình thoi
=>AC vuông góc BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại O và O là trung điểm chung của AC và BD
Xét tứ giác OCED có
F là trung điểm chung của OE và CD
Do đó: OCED là hình bình hành
mà góc DOC=90 độ(AC vuông góc BD tại O)
nên OCED là hình chữ nhật
=>DE//OC và DE=OC
=>DE//OA và DE=OA(Do OC=OA)
Xét tứ giác AOED có
AO//ED
AO=ED
Do đó: AOED là hình bình hành
b: Xét tứ giác BDSC có
F là trung điểm chung của DC và BS
Do đó: BDSC là hình bình hành
=>CS//BD
mà CE//BD
và CS cắt CE tại C
nên C,S,E thẳng hàng
c: Để BDSC là hình thoi thì BD=BC
BD=CS(BDSC là hình bình hành)
OD=CE(ODEC là hình chữ nhật)
=>BD=2CE
=>CS=2CE
=>E là trung điểm của CS
=>ES/BD=1/2
Xét ΔKBD và ΔKSE có
góc KBD=góc KSE
góc BKD=góc SKE
Do đó: ΔKBD đồng dạng với ΔKSE
=>KD/KE=BD/SE=2
15 tháng 4 2020
Theo giả thiết thì AB = BC = CD = AD = AC
\(\Rightarrow\Delta ABC\)và \(\Delta ACD\)đều
vì BC // ED \(\Rightarrow\widehat{BCF}=\widehat{ADC}=60^o\)
AB // DF \(\Rightarrow\widehat{EAB}=\widehat{ADC}=60^o\)
\(\Rightarrow\widehat{EAC}=\widehat{ACF}=120^o\)
\(\Delta ABE~\Delta DFE\); \(\Delta CFB~\Delta DFE\)
\(\Rightarrow\Delta ABE~\Delta CFB\Rightarrow\frac{AB}{AE}=\frac{CF}{BC}\Rightarrow CF.AE=AB.BC=AC^2\)
\(\Rightarrow\frac{AC}{CF}=\frac{AE}{AC}\)
\(\Rightarrow\Delta ACE~\Delta CFA\left(c.g.c\right)\Rightarrow\widehat{CFA}=\widehat{ACE}\)
Ta có : \(\widehat{OAC}+\widehat{OCA}=\widehat{OAC}+\widehat{CFA}=60^o\)
\(\Rightarrow\widehat{AOC}=\widehat{ÈOF}=120^o\)
14 tháng 12 2022
a: \(AC=\sqrt{15^2+8^2}=17\left(cm\right)\)
OD=AC/2=8,5cm
b: Xét tứ giác ADPC có
M là trung điểm chung của AP và DC
nên ADPC là hình bình hành
=>DP=AC=2OC
c: Xét tứ giác OBEC có
N là trung điểm chung của OE và bC
OB=OC
Do dó: OBEC là hình thoi