Bài 2: Cho tam giác ABC có AB = 8cm, M là trung điểm của AC, N là trung điểm của BC. Tính MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 1 2022
Bài 1:
Xét tứ giác ABCD:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{o}\) (Tổng các góc trong tứ giác).
Mà \(\widehat{A}= \) \(57^o;\) \(\widehat{C}=\) \(110^o;\) \(\widehat{D}=\) \(75^o\left(gt\right).\)
\(\Rightarrow\) \(\widehat{B}=\) \(118^o.\)
17 tháng 12 2023
Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{BC}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Ta có: AB=AC
\(AM=MB=\dfrac{AB}{2}\)(M là trung điểm của AB)
\(AN=NC=\dfrac{AC}{2}\)(N là trung điểm của AC)
Do đó: \(AM=MB=AN=NC=\dfrac{AB}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Kẻ AH\(\perp\)MN tại H
Ta có: AH\(\perp\)MN
CE\(\perp\)MN
Do đó: AH//CE
Ta có: ΔAMN cân tại A
mà AH là đường cao
nên H là trung điểm của MN
=>\(HM=HN=\dfrac{MN}{2}=2\left(cm\right)\)
Ta có: ΔAHN vuông tại H
=>\(AH^2+HN^2=AN^2\)
=>\(AH^2+2^2=5^2\)
=>\(AH^2=25-4=21\)
=>\(AH=\sqrt{21}\left(cm\right)\)
Xét ΔNAH vuông tại H và ΔNCE vuông tại E có
NA=NC
\(\widehat{ANH}=\widehat{CNE}\)
Do đó: ΔNAH=ΔNCE
=>\(AH=CE=\sqrt{21}\left(cm\right)\)
CM
20 tháng 3 2017
* Ta có: A B 2 + A C 2 = B C 2 ( 6 2 + 8 2 = 10 2 = 100 )
Suy ra: tam giác ABC vuông tại A
⇒ AB ⊥ AC
* Lại có: MN ⊥ AB nên MN // AC.
* Vì MN // AC và M là trung điểm của BC nên N là trung điểm của AB.
Khi đó, MN là đường trung bình của tam giác ABC .
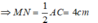
Chọn đáp án A
9 tháng 7 2020
Cho 2 cái hình vì con chưa hc lp 8.
Bài 1
A B C M N
Bài 2 : G A B C M D E
25 tháng 10 2021
a: Xét hình thang BDEC có
M là trung điểm của BD
N là trung điểm của EC
Do đó: MN là đường trung bình của hình thang BDEC
Suy ra: \(MN=\dfrac{DE+BC}{2}=\dfrac{8+4}{2}=6\left(cm\right)\)
2 tháng 4 2020
a) Ta có
+)AM=AB-BM=6-3,75=2,25
+)MN//BC => \(\frac{AN}{AC}=\frac{AM}{AB}\)=> \(\frac{AN}{8}=\frac{2,25}{6}=\frac{3}{8}\)
=> AN=3(cm)
CN=AC-AN=8-3=5(cm)
b) +)MK//BI => \(\frac{MK}{BI}=\frac{AK}{AI}\left(1\right)\)
+) NK//CI => \(\frac{NK}{CI}=\frac{AK}{AI}\left(2\right)\)
(1)(2) => \(\frac{MK}{BI}=\frac{NK}{CI}\)mà MK=NK (K là trung điểm MN)
=> BI=CI => I là trung điểm BC
c) \(\Delta\)ABC vuông tại A
=> BC2=AB2+AC2=62+82=102 (Định lý Pytago)
=> BC=10cm
Ta có: \(\hept{\begin{cases}\frac{AN}{CN}=\frac{3}{5}\\\frac{AB}{BC}=\frac{6}{10}=\frac{3}{5}\end{cases}\Rightarrow\frac{AN}{CN}=\frac{AB}{AC}=\frac{3}{5}}\)
=> BN là phân giác \(\widehat{ABC}\)
Xét tam giác ABC có:
M là trung điểm của AC
N là trung điểm của BC
=> MN là đường trung bình của tam giác ABC
=> MN = 1/2 . AB = 1/2 . 8 = 4 (cm)