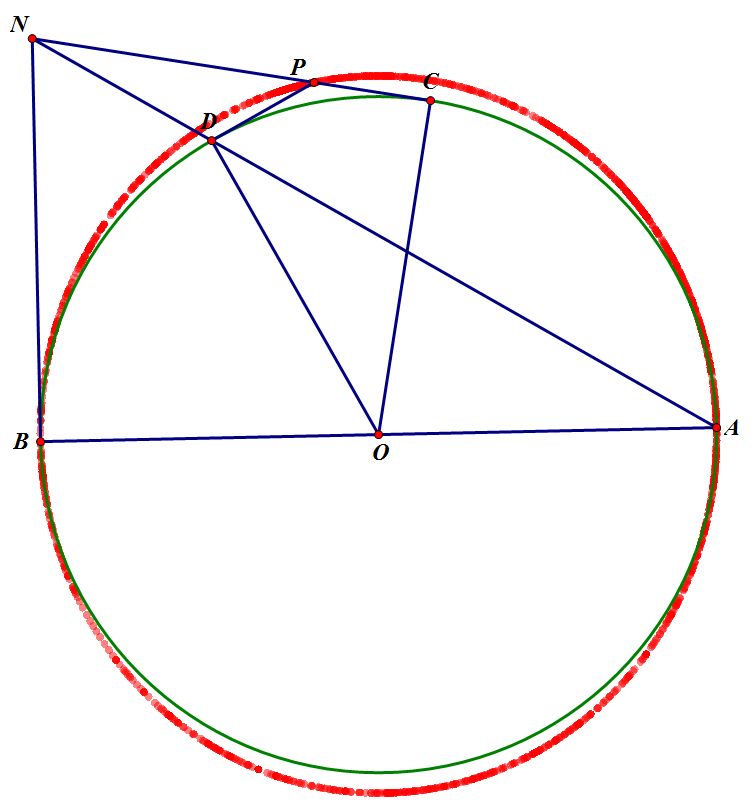
Cho C thuộc (O) đường kính AB,tiếp tuyến tại B và C cắt nhau tại N,NA cắt (O) tại D,tiếp tuyến tại D cắt ON tại P.chứng minh P di động trên đường cố định khi C di động trên (O)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 1 2017
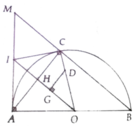
a, HS tự chứng minh
b, Ta có: I A C ^ = I C A ^ => I M C ^ = I C M ^ nếu IM = IA = IC
c, Sử dụng hệ thức lượng cho ∆AMB ta dùng Pytago cho tam giác AMB
d, Kẻ GD//AC (D ∈ OC) => D cố định lại có OI ⊥ AC => OG ⊥ DG
=> G thuộc đường tròn đường kính OD cố định
18 tháng 12 2016
Mình chỉ nói gợi ý thôi, bạn tự phát triển nhé:
Câu a)
- CM: \(MO\)song song với \(NB\).
- CM: tam giác \(MAO\) và \(NOB\) bằng nhau.
- CM: \(OMNB\) là hình bình hành.
Câu b)
- CM: \(MAON\)là hình chữ nhật.
- CM: \(H\) là giao của \(MO\) và \(AN\)
- Gọi \(D\) là hình chiếu của \(H\) lên \(AB\). CM: \(D\) là trung điểm \(AO\).
- CM: \(H\) di động trên đường cố định.
22 tháng 4 2021
a)Xét tứ giác MBOC có
\(\widehat{OBM}\) và \(\widehat{OCM}\) là hai góc đối
\(\widehat{OBM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MBOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
14 tháng 2 2017
Tự vẽ hình:
a) ta có: Nx là tiếp tuyến => \(\widehat{PNO}=90\)
d\(⊥\)AB=> \(\widehat{OMP}=90\)
=> tứ giác OMNP nội tiếp
b) Ta có: CO II MP ( cùng vuông góc với AB)
Tứ giác OMNP nội tiếp => \(\widehat{OPM}=\widehat{ONM}\) (1)
Tam giác cân OCN ( OC=ON=R) có: \(\widehat{OCN}=\widehat{ONM}\) (2)
Từ (1), (2) => \(\widehat{OPM}=\widehat{OCM}\)(**)
Từ (*), (**) => OCMP là hình bình hành
c) Xét \(\Delta OCN\)là tam giác cân
và \(\Delta MCD\)là tam giác cân ( do C,D đối xứng nhau qua AB) có chung góc C
=> \(\Delta OCN\)đồng dạng \(\Delta MCD\)
=>\(\frac{CN}{CD}=\frac{OC}{CM}\Rightarrow CN.CM=OC.CD=2R^2=const\)
Vậy CN.CM không đổi (ĐPCM)
CM
16 tháng 11 2019
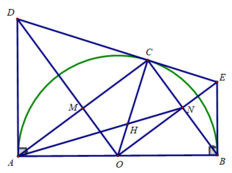
d) Ta có: N là trung điểm của BC
⇒ AN là trung tuyến của ΔABC
CO cũng là trung tuyến của ΔABC
AN ∩ CO = H
⇒ H là trọng tâm ΔABC
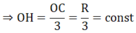
Vậy khi C di chuyển trên nửa đường tròn (O) thì H di chuyển trên nửa đường tròn
(O; R/3)