Cho tam giác ABC có 3 góc nhọn. Kẻ AH vuông góc với BC H thuộc BC. Qua H kẻ HM vuông góc với AB (M thuộc BA). Trên tia đối của tia MH lấy E sao cho ME = MH. a)Chứng minh rằng: tam giác AEM =tam giác AHMb)Chứng minh rằng: AE vuông góc EB c)Qua H kẻ HN vuông góc với AC (N thuộc CA), trên tia đối của tia NH lấy F sao cho NF = NH. Chứng minh rằng: AE = AF. d)Chứng minh rằng: BC = BE + CF.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAEM vuông tại M và ΔAHM vuông tại M có
AM chung
ME=MH
Do đó: ΔAEM=ΔAHM
b: Xét ΔBHE có
BM là đường cao
BM là đường trung tuyến
Do đó: ΔBHE cân tại B
Xét ΔAEB và ΔAHB có
AE=AH
EB=HB
AB chung
Do đó: ΔAEB=ΔAHB
Suy ra: \(\widehat{AEB}=\widehat{AHB}=90^0\)
hay AE⊥EB

a: Xét ΔAME vuông tại M và ΔAMH vuông tại M có
AM chung
ME=MH
=>ΔAME=ΔAMH
b: Xét ΔAHF có
AC vừa là đường cao, vừa là trung tuyến
=>ΔAHF cân tại A
=>AC là phân giác của góc FAH
góc FAE=góc FAH+góc EAH
=2*(góc BAH+góc CAH)
=180 độ
=>F,A,E thẳng hàng
mà AE=AF
nên A là trung điểm của FE

1: Xét ΔAHD có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔAHD cân tại A
mà AN là đường cao
nên AN là đường phân giác(1)
Xét ΔAHE có
AM là đường cao
AM là đường trung tuyến
Do đó: ΔAHE cân tại A
mà AM là đường cao
nên AM là đường phân giác(2)
Từ (1) và (2) suy ra \(\widehat{DAE}=2\cdot\left(\widehat{MAH}+\widehat{NAH}\right)=2\cdot90^0=180^0\)
=>D,A,E thẳng hàng
2: Xét ΔHED có
M là trung điểm của HE
N là trung điểm của HD
Do đó: MN là đường trung bình
=>MN//ED

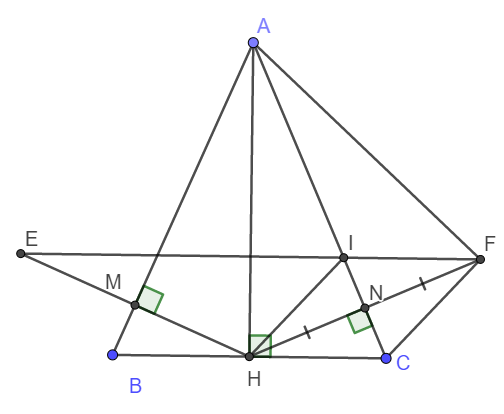
a) Do ABC là tam giác cân tại A nên AH là đường cao hay đồng thời là đường phân giác.
Xét tam giác vuông AMH và tam giác vuông ANH có:
Cạnh AH chung
\(\widehat{MAH}=\widehat{NAH}\)
\(\Rightarrow\Delta AMH=\Delta ANH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HM=HN.\)
b) Dễ dàng thấy ngay AC là đường trung trực của HF.
Khi đó thì AH = AF; CH = CF
Xét tam giác AHC và tam giác AFC có:
Cạnh AC chung
AH - AF
CH = CF
\(\Rightarrow\Delta AHC=\Delta AFC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFC}=\widehat{AHC}=90^o\Rightarrow AF\perp CF.\)
c) Ta thấy ngay \(\Delta HIN=\Delta FCN\left(g-c-g\right)\)
\(\Rightarrow IN=CN\)
Xét tam giác vuông INF và tam giác vuông CNH có:
HN = FN
IN = CN
\(\Rightarrow\Delta INF=\Delta CNH\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{IFN}=\widehat{CHN}\)
Mà chúng lại ở vị trí so le trong nên IF // BC.
d) Chứng minh tương tự câu c, ta có IE // BC
Vậy thì qua I có hai tia IE và IF cùng song song với BC nên chúng trùng nhau.
Vậy I, E, F thẳng hàng.

1: Xét ΔAHE có
AM là đường cao
AM là đường trung tuyến
Do đó: ΔAHE cân tại A
mà AM là đường cao
nên AM là đường phân giác(1)
Xét ΔAHD có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔAHD cân tại A
mà AN là đường cao
nên AN là đường phân giác(2)
Từ (1) và (2) suy ra \(\widehat{DAE}=2\cdot\left(\widehat{MAH}+\widehat{NAH}\right)=2\cdot90^0=180^0\)
hay D,A,E thẳng hàng
2: Xét ΔHED có
M là trung điểm của HE
N là trung điểm của HD
Do đó: MN là đường trung bình
=>MN//ED
4: Ta có: AH=AD
mà AH=AE
nên AD=AE=AH

a, Xét tam giác vuông MHC có :
\(\widehat{CMH}+\widehat{HCM}=90^o\)
Xét tam giác vuông ABC có:
\(\widehat{HIB}+\widehat{HCM}=90^o\)
\(\Rightarrow\widehat{CMH}=\widehat{HIB}\)
Xét 2 tam giác : KHM và IHB
MH = HB ( gt )
\(\widehat{CMN}=\widehat{HBI}\left(cmt\right)\)
\(\widehat{MKH}=\widehat{HIB}=90^o\)
\(\Rightarrow\Delta KHM=\Delta IHB\)
b, \(\Rightarrow HK=HI\)
Xét 2 tam giác : KHA và IHA
KM = IH ( cm a )
AN chung
\(\widehat{HKA}=\widehat{AIM}=90^o\)
\(\Rightarrow\Delta KHA=\Delta IHA\)
\(\Rightarrow\widehat{KAH}=\widehat{HAI}\)
Vậy : AH là tia phân giác góc BAC
a, xet △ vuong mhc co ∠cmh + ∠hcm = 90 do xet △ vuong abc co ∠hbi + ∠hcm = 90 do suy ra ∠cmh = ∠hbi xet △ BHI va △ MHK co ∠CMH = ∠HBI [c/m tr] HM = BH [gt] ∠BIH = ∠MKH [=90 do] ➩ △ BHI = △ MHK [ch-gn] b, tu a co △bhi = △mhk ➩ ih = kh xet △aih va △akh co ah chung ih = kh [c/m tr] ∠aih = ∠akh [= 90 do] ➩ △aih = △kah [ch-cgv] ➩ ∠iah = ∠kah ➩ ah la p/g cua ∠bac
a: Xét ΔAEM vuông tại M và ΔAHM vuông tại M có
AM chung
ME=MH
Do đó: ΔAEM=ΔAHM
b: Xét ΔBHE có
BM là đường cao
BM là đường trung tuyến
Do đó: ΔBHE cân tại B
Xét ΔAEB và ΔAHB có
AE=AH
EB=HB
AB chung
Do đó: ΔAEB=ΔAHB
Suy ra: \(\widehat{AEB}=\widehat{AHB}=90^0\)
hay AE⊥EB