giúp em với em đang cần gấp huhu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
\(\left(4x+3\right)\left(3x^2+x-2\right)\left(2x^2-3x-5\right)=0\\ \Leftrightarrow\left(4x+3\right)\left(3x-2\right)\left(x+1\right)\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=-1\\x=\dfrac{2}{3}\\x=\dfrac{5}{2}\end{matrix}\right.\\ \Leftrightarrow A=\left\{-1;-\dfrac{3}{4};\dfrac{2}{3};\dfrac{5}{2}\right\}\)
Câu 2:
\(\left(x^2-4\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=3\end{matrix}\right.\Leftrightarrow A=\left\{-2;2;3\right\}\\ \left|5x\right|-11\le0\Leftrightarrow\left|5x\right|\le11\Leftrightarrow-11\le5x\le11\\ \Leftrightarrow-\dfrac{11}{5}\le x\le\dfrac{11}{5}\\ \Leftrightarrow B=\left[-\dfrac{11}{5};\dfrac{11}{5}\right]\)
\(\Leftrightarrow A\cap B=\left\{-2;2\right\}\\ A\cup B=\left[-\dfrac{11}{5};3\right]\\ A\B=\left\{3\right\}\)

1.
a.
\(n^2+7n+1=k^2\Rightarrow4n^2+28n+4=4k^2\)
\(\Leftrightarrow\left(2n+7\right)^2-45=\left(2k\right)^2\)
\(\Leftrightarrow\left(2n-2k+7\right)\left(2n+2k+7\right)=45\)
Phương trình ước số cơ bản
b.
\(a^3b^3+b^3-3ab^2=-1\)
\(\Leftrightarrow a^3+1-\dfrac{3a}{b}=-\dfrac{1}{b^3}\)
\(\Leftrightarrow a^3+\dfrac{1}{b^3}+1-\dfrac{3a}{b}=0\)
Đặt \(\left(a;\dfrac{1}{b}\right)=\left(x;y\right)\Rightarrow x^3+y^3+1-3xy=0\)
\(\Leftrightarrow\left(x+y\right)^3+1-3xy\left(x+y\right)-3xy=0\)
\(\Leftrightarrow\left(x+y+1\right)\left(x^2+y^2+1-xy-x-y\right)=0\)
\(\Leftrightarrow x+y+1=0\)
\(\Rightarrow P=a+\dfrac{1}{b}=x+y=-1\)
2.
a.
\(a+b+\dfrac{1}{a}+\dfrac{1}{b}=\left(\dfrac{a}{4}+\dfrac{1}{a}\right)+\left(\dfrac{b}{4}+\dfrac{1}{b}\right)+\dfrac{3}{4}\left(a+b\right)\)
\(\ge2\sqrt{\dfrac{a}{4a}}+2\sqrt{\dfrac{b}{4b}}+\dfrac{3}{4}.4=5\) (đpcm)
Dấu "=" xảy ra khi \(a=b=2\)

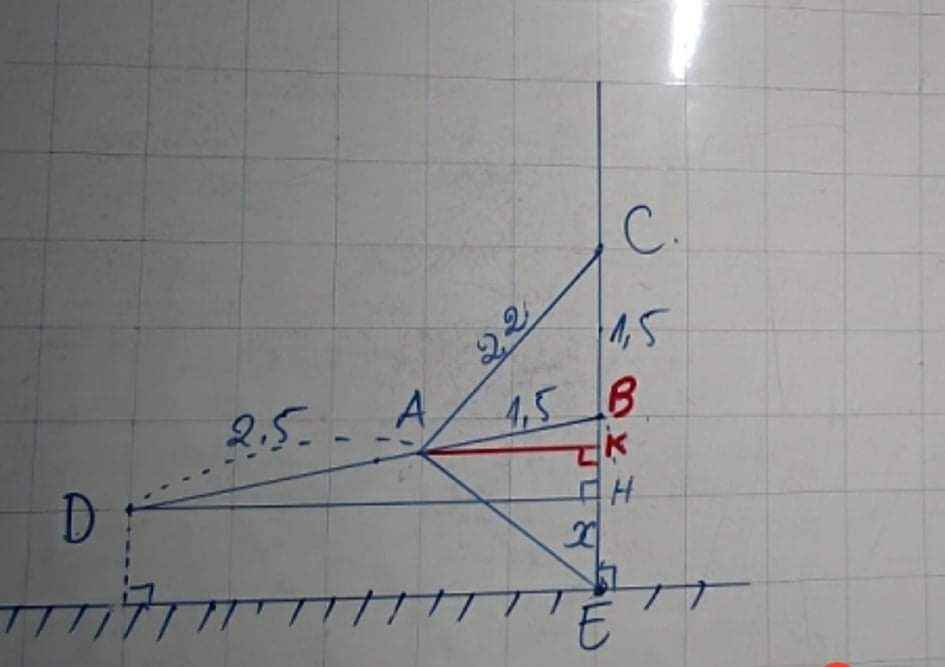
C A B E D H K
Gọi DH là khoảng cách thấp nhất từ máy bay đến mặt đất, khi đó AC có độ dài lớn nhất là 2,2m. Dựng hình chữ nhật DHEK => DH = EK
Do BA = BE = BC = 1,5m cố định nên tam giác ACE vuông tại A
Xét tam giác ACE vuông tại A có cos\(\widehat{ECA}\) = \(\dfrac{CA}{CE}=\dfrac{2,2}{3}\) => \(\widehat{ECA}\) \(\approx\) 42o50'
BA = BC => tam giác ABC cân tại B => \(\widehat{BAC}=\widehat{BCA}\) = \(\widehat{ECA}\) \(\approx\) 42o50'
=> \(\widehat{DBK}\) = \(\widehat{BAC}+\widehat{BCA}\) = 2.\(\widehat{BCA}\) = 85o40'
Xét tam giác DBK vuông tại D có: BK = BD. cos\(\widehat{DBK}\)
= 4.cos85o40' \(\approx\) 0,3022
=> DH = KE \(\approx\) 1,5 - 0,3022 \(\approx\)1,2 (m)


Bài 1:
a, \(\dfrac{2}{3}\) + \(\dfrac{1}{5}\). \(\dfrac{10}{7}\)
= \(\dfrac{2}{3}\) + \(\dfrac{2}{7}\)
= \(\dfrac{20}{21}\)
b, \(\dfrac{7}{12}\) - \(\dfrac{27}{7}\). \(\dfrac{1}{18}\)
= \(\dfrac{7}{12}\) - \(\dfrac{3}{14}\)
= \(\dfrac{31}{84}\)
c, \(\dfrac{3}{10}\). \(\dfrac{-5}{6}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{1}{4}\) - \(\dfrac{1}{8}\)
= - \(\dfrac{3}{8}\)
d, - \(\dfrac{4}{9}\): \(\dfrac{8}{3}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{6}\) + \(\dfrac{1}{18}\)
= - \(\dfrac{1}{9}\)
e, {[(\(\dfrac{1}{2}\) - \(\dfrac{2}{3}\))2 : 2 ] - 1}. \(\dfrac{4}{5}\)
= {[ (-\(\dfrac{1}{6}\))2 : 2] - 1}. \(\dfrac{4}{5}\)
= { [\(\dfrac{1}{36}\) : 2] - 1}. \(\dfrac{4}{5}\)
= { \(\dfrac{1}{72}\) - 1}. \(\dfrac{4}{5}\)
=- \(\dfrac{71}{72}\).\(\dfrac{4}{5}\)
= -\(\dfrac{71}{90}\)


\(\frac{-5}{6}\)\(+\)\(\frac{4}{9}\)\(\times\)\(\left(\frac{5}{4}-\frac{2}{3}\right)\)\(\times\)\(\left(-3\right)^2\)\(+\)\(\frac{5}{9}\)\(\times\)\(30\%\)
\(=\)\(\frac{-5}{6}\)\(+\)\(\frac{4}{9}\)\(\times\)\(\frac{7}{12}\)\(\times\)\(9\)\(+\)\(\frac{5}{9}\)\(\times\)\(\frac{3}{10}\)
\(=\)\(\frac{-5}{6}\)\(+\)\(\frac{7}{3}\)\(+\)\(\frac{5}{9}\)\(\times\)\(\frac{3}{10}\)
\(=\)\(\frac{-5}{6}\)\(+\)\(\frac{7}{3}\)\(+\)\(\frac{1}{6}\)
\(=\)\(\frac{-5}{6}\)\(+\)\(\frac{1}{6}\)\(+\)\(\frac{7}{3}\)
\(=\)\(\frac{-2}{3}\)\(+\)\(\frac{7}{3}\)
\(=\)\(\frac{5}{3}\)