Trong không gian \(Oxyz\), cho các điểm \(A\left(-2;1;2\right);B\left(2;1;-2\right)\)và \(C\left(1;1;1\right)\)Gọi d là đường thẳng đi qua C sao cho tổng khoảng cách từ A và B đến d lớn nhất. Khi đó giao điểm của d với mặt phẳng \(\left(P\right):2x+y+z=0\)có tọa độ là gì?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trục Ox nhận \(\left(1;0;0\right)\) là 1 vtcp
Do đó mặt phẳng vuông góc Ox nhận \(\left(1;0;0\right)\) là 1 vtpt
Phương trình:
\(1\left(x+1\right)+0\left(y-2\right)+0\left(z-1\right)=0\)
\(\Leftrightarrow x+1=0\)

Đáp án A.
Phương pháp:
+) Cho hai điểm ![]()
Khi đó ta có: ![]()
Cách giải:
Ta có:
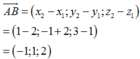

Đáp án D
Với điểm A(2;-3;4). Hình chiếu của A trên 3 trục tọa độ lần lượt là:
B(2; 0; 0); C( 0; -3; 0) và D( 0; 0; 4).
Phương trình mặt phẳng (BCD) là:
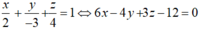

Đáp án B
Phương pháp:
Hình chiếu của điểm M(x0;y0;z0) trên trục Ox là điểm M1(x0;0;0)
Hình chiếu của điểm M(x0;y0;z0) trên trục Oy là điểm M2(0;y0;0)
Hình chiếu của điểm M(x0;y0;z0) trên trục Oz là điểm M3(0;0;z0)
Phương trình theo đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c), (a,b,c ≠ 0) là: x a + y b + z c = 1
Cách giải: Hình chiếu của điểm A(2; –1;1) trên các trục tọa độ Ox, Oy, Oz lần lượt là: (2;0;0), (0; –1;0), (0;0;1)
Phương trình mặt phẳng (α): x 2 + y - 1 + z 1 = 1

Đáp án B
Phương pháp:
Hình chiếu của điểm M ( x 0 ; y 0 ; z 0 ) trên trục Ox là điểm M 1 ( x 0 ; 0 ; 0 )
Hình chiếu của điểm M ( x 0 ; y 0 ; z 0 ) trên trục Oy là điểm M 2 ( 0 ; y 0 ; 0 )
Hình chiếu của điểm M ( x 0 ; y 0 ; z 0 ) trên trục Oz là điểm M 3 ( 0 ; 0 ; z 0 )
Phương trình theo đoạn chắn của mặt phẳng đi qua 3 điểm A(a;0;0), B(0;b;0), C(0;0;c) (a,b,c ≠ 0 ) là
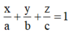
Cách giải: Hình chiếu của điểm A(2;-1;1) trên các trục tọa độ Ox, Oy, Oz lần lượt là: (2;0;0), (0;-1;0),(0;0;1).
Phương trình mặt phẳng α : x 2 + y - 1 + z 1 = 1

Giả sử ta có M (a;0;0); N (0;b;0) và P (0;0;c) với a,b,c > 0.
\(\Rightarrow V_{OMNP}=\dfrac{1}{6}abc\)
\(\Rightarrow\left(\alpha\right)\) có dạng \(\dfrac{2}{a}+\dfrac{1}{b}+\dfrac{3}{c}=1\) do mặt phẳng đi qua điểm A (2;1;3).
Mặt khác, theo bất đẳng thức Cauchy:
\(1=\dfrac{2}{a}+\dfrac{1}{b}+\dfrac{3}{c}\ge3\sqrt[3]{\dfrac{2.1.3}{abc}}\)
\(\Leftrightarrow abc\ge162\)
\(\Rightarrow V\ge27\).
Dấu bằng xảy ra khi và chỉ khi \(\dfrac{2}{a}=\dfrac{1}{b}=\dfrac{3}{c}=\dfrac{1}{3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=3\\c=9\end{matrix}\right.\)
\(\Rightarrow\left(\alpha\right):\dfrac{x}{6}+\dfrac{y}{3}+\dfrac{z}{9}=1\)
Có phương trình đường thẳng d, giao điểm của đường thẳng d với mặt phẳng \(\alpha\) là nghiệm của hệ phương trình (d) và \(\left(\alpha\right)\). Như vậy, x = 4, y = -1 và z = 6.
Chọn A.
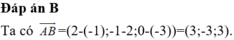


<666> ma trong olm 3 sáng