1. Cho tam giác nhọn ABC có M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh ΔAMB = ΔDMC
b) Chứng minh AB // CD
c) Từ M vẽ MH ⊥ AB (H ϵ AB), MK ⊥ CD (K ϵ CD). Chứng minh 3 điểm H,M,K thẳng hàng.
CHỈ CẦN GIẢI GIÚP MÌNH CÂU C THÔI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AMB = 
AB (H
AB), MK 
5 tháng 1 2022
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 2 2018
a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)
18 tháng 12 2021
b: Xét tứ giác ABDC có
M là trung điểm của DA
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
1K
18 tháng 12 2021
cho em xin cái hình đc ko ạ em ko bit hình em vẽ đúng hay sai nữa ạ.
16 tháng 1 2022
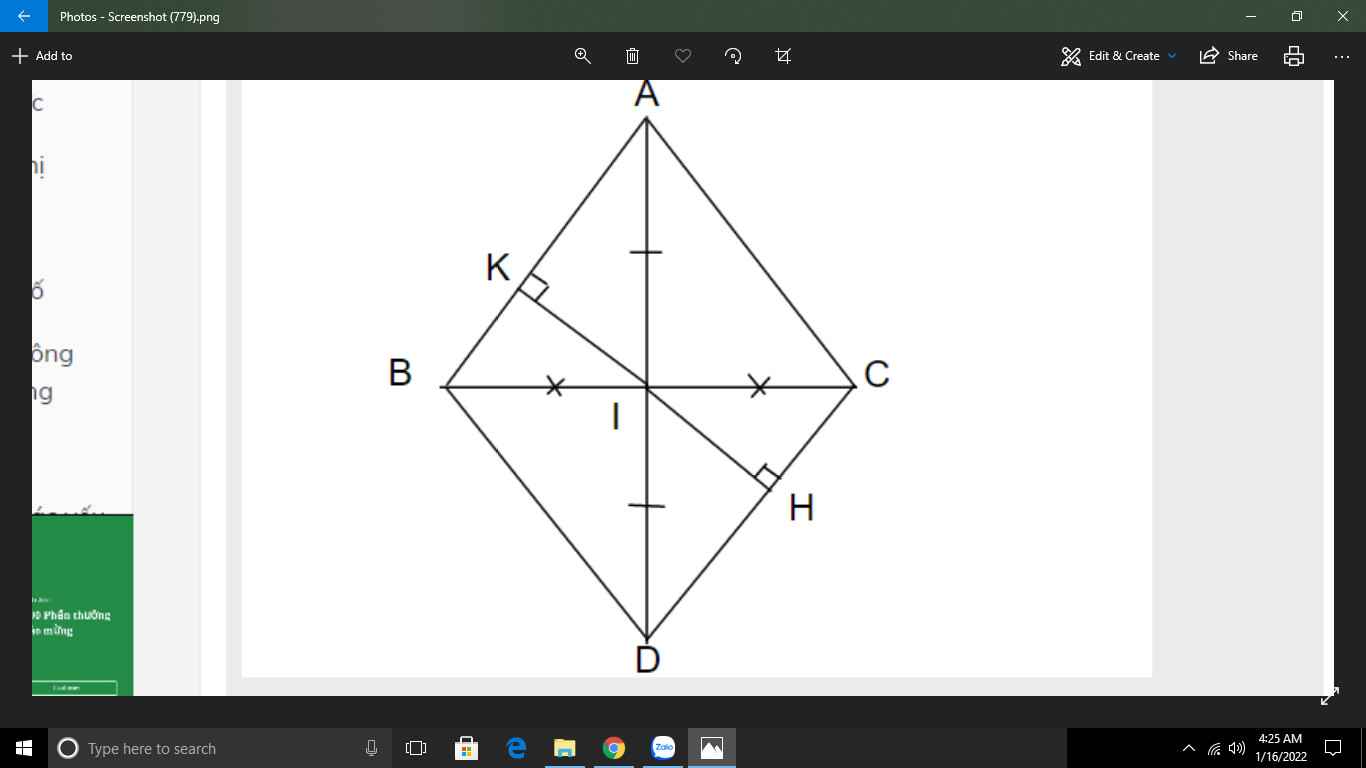
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)
16 tháng 12 2021
a: Xét ΔAMB và ΔCMD có
MB=MD
\(\widehat{AMB}=\widehat{CMD}\)
MA=MC
Do đó: ΔAMB=ΔCMD
22 tháng 1 2022
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB=CD và AB//CD
b: Ta có: ABDC là hình bình hành
nên BD//AC
c: Ta có: AB//CD
nên \(\widehat{ABC}=\widehat{DCB}\)
9 tháng 1 2022
a: Xét ΔABM và ΔACM có
AM chung
AB=AC
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét tứ giác ABDC có
M là trung điểm của BC
M la trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
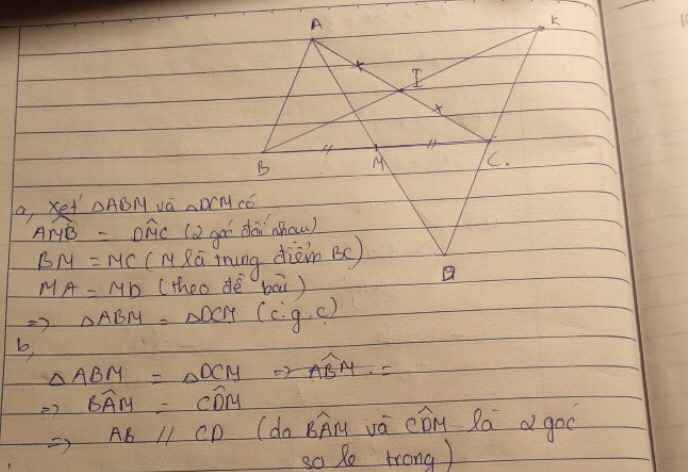
c: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có
MB=MC
\(\widehat{MBH}=\widehat{MCK}\)
Do đó; ΔMHB=ΔMKC
Suy ra: BH=CK
Xét tứ giác HBKC có
HB//KC
HB=KC
Do đó: HBKC là hình bình hành
SUy ra: HK và BC cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
hay H,M,K thẳng hàng