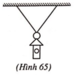
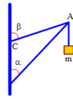
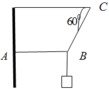
Cho một hệ vật như hình 1.1.1. Dây chỉ có thể chịu lực căng dây tối đa là 20 N. Thanh nặng 3 kg. Hỏi dây cần phải treo hợp với tường một góc nhỏ nhất là bao nhiêu để có thể cân bằng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

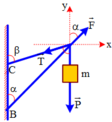
Chọn chiều dương hướng lên trên. Các lực tác dụng lên vật gồm trọng lực P→ và sức căng dây T→ của sợi dây.
Định luật II Niuton: P→+T→=ma→(∗)
Chiếu (*) lên chiều dương: −P+T=ma
⇒T=P+ma=m(g+a)⇒T=P+ma=m(g+a)
Dây không bị đứt khi : T≤Tmax
⇒m(g+a)≤55
⇒5(10+a)≤55
⇒a≤1(m/s2 )

a)
+ Vật cân bằng nên: 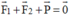 (1,50 điểm)
(1,50 điểm)
+ Chiếu phương lên trục Oy thẳng đứng ta được:
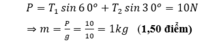
b) Theo điều kiện cân bằng của Momen lực: 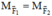
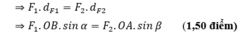
+ OB = OA + AB = 50 cm


Chọn đáp án B
? Lời giải:
Cách 1: Biểu diễn các lực như hình vẽ:
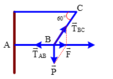
+ Theo điều kiện cân bằng:
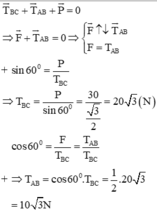
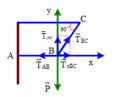
+ Chọn hệ quy chiếu Oxy như hình vẽ.


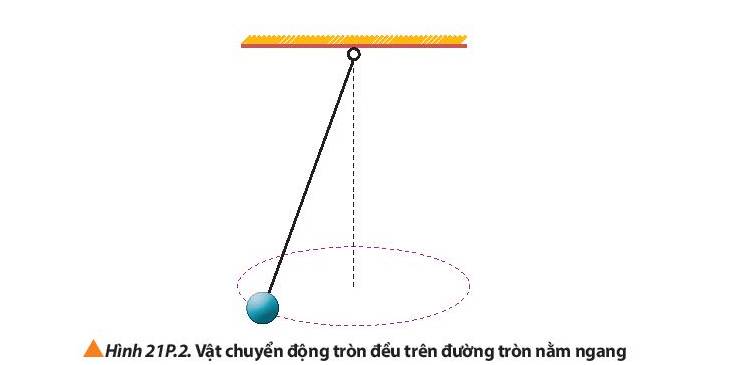
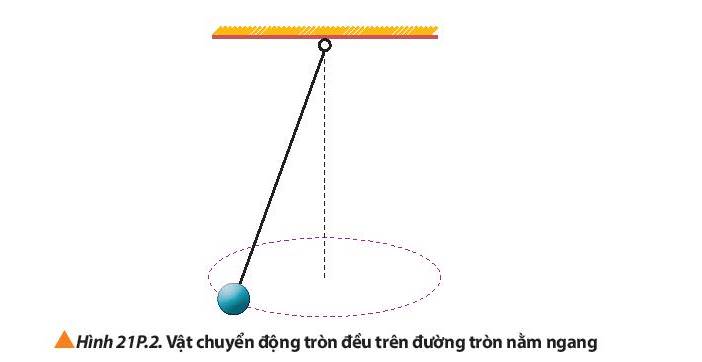
Lực đóng vai trò là lực hướng tâm trong trường hợp trên là lực căng.
=> Vận tốc cực đại của vật để dây không bị đứt là:
\(\begin{array}{l}{T_{\max }} = {F_{ht\max }} = m.\frac{{v_{\max }^2}}{R}\\ \Rightarrow {v_{\max }} = \sqrt {\frac{{{T_{\max }}.R}}{m}} = \sqrt {\frac{{50.1,5}}{{0,5}}} \approx 12,23(m/s)\end{array}\)

Chọn B.
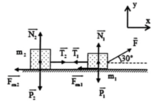
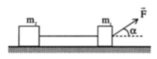
Các lực tác dụng vào hệ như hình vẽ. Áp dụng định luật II Newton chp từng vật ta được
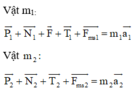
Chiếu vecto lên trục tọa độ đã chọn trên hình
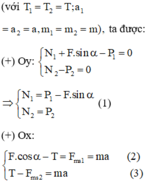
Từ công thức lực ma sát, kết hợp (1) ta có:
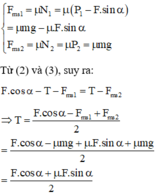
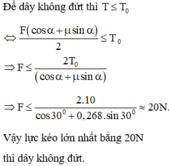

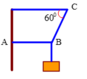
Ta có P = mg = 3.10=30 (N)
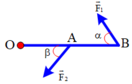
Biểu diễn các lực như hình vẽ
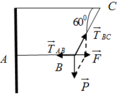
Theo điều kiện cân bằng
T → B C + T → A B + P → = 0 ⇒ F → + T → A B = 0
⇒ F → ↑ ↓ T → A B F = T A B
Ta có S i n 60 0 = P T B C
⇒ T B C = P S i n 60 0 = 30 3 2 = 20 3 ( N )
C o s 60 0 = F T B C = T A B T B C ⇒ T A B = C o s 60 0 . T B C = 1 2 .20. 3 = 10 3 ( N )
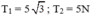 . Vật có khối lượng là bao nhiêu?
. Vật có khối lượng là bao nhiêu?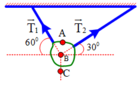
 . Tính F2
. Tính F2