Cho (O) đường kính BC, điểm A nằm trên cung BC. Trên tia AC lấy điểm D sao cho AB = AD. Dựng hình vuông ABED; AE cắt (O) tại điểm thứ hai F; Tiếp tuyến tại B cắt đường thẳng DE tại G.
1/ CMR: tứ giác BGDC nội tiếp. Xác định tâm I của đường tròn này.
2/ CMR: BFC vuông cân và F là tâm đường tròn ngoại tiếp BCD.
3/ CMR: Tứ giác GEFB nội tiếp.
4/ Chứng tỏ: C; F; G thẳng hàng và G cũng nằm trên đường tròn ngoại tiếp BCD. Có nhận xét gì về I và F
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

△ABC nội tiếp đường tròn đường kính BC.
\(\Rightarrow\)△ABC vuông tại A.
- Ta có: \(\widehat{ABC}+\widehat{ABG}=90^0\) (\(BG\perp BC\) tại B).
\(\widehat{EBG}+\widehat{ABG}=90^0\) (\(AB\perp EB\) tại B).
\(\Rightarrow\widehat{ABC}=\widehat{EBG}\)
△ABC và △EBG có: \(\widehat{ABC}=\widehat{EBG}\) (cmt)
\(AB=EB\) (ABED là hình vuông).
\(\widehat{BAC}=\widehat{BEG}=90^0\)
\(\Rightarrow\)△ABC=△EBG (g-c-g).
\(\Rightarrow\widehat{ACB}=\widehat{EGB}\) (1).
AFBC là tứ giác nội tiếp có \(\widehat{EFB}\) là góc ngoài đỉnh F.
\(\Rightarrow\widehat{ACB}=\widehat{EFB}\) (2).
(1), (2) \(\Rightarrow\widehat{EGB}=\widehat{EFB}\) nên GEBF nội tiếp.

a. Do AE là đường chéo hinh vuông nên \(\widehat{BAE}=\widehat{EAD}\Rightarrow\widehat{BAF}=\widehat{FAC}\)
Chúng lại là hai góc nội tiếp chắn cũng BF và FC nên cung FB = FC.
Vậy dây FB = FC, mà \(\widehat{BFC}=90^o\) (Do BC là đường kính) nên tam giác FBC vuông cân tại F.
b) Do ABED là hình vuông nên AE vuông góc BD tại trung điểm mỗi đường. Vậy tam giác BFD cân tại F hay FB = FD.
Do câu a: FB = FC nên FC = FD.
c) Gọi G là giao điểm của CF và tiếp tuyến tại B của đường tròn đường kính BC. Khi đó G cố định.
Gọi H là giao điểm của BE với đường tròn. Ta thấy ngay ABHC là hình chữ nhật nên AC = BH hay cung AC = cung BH.
Khi đó \(\widehat{GBE}=\widehat{AFC}=\widehat{GFE}\) nên tứ giác BFEG nội tiếp. Suy ra E thuộc đường tròn qua ba điểm B, G, F.
Giải bài toán hình Cho (O) đường kính BC và một điểm A nằm trên cung BC sao cho AB>AC.Trên tia AC lấy điểm D sao cho AD=AB, vẽ hình vuông BADE,tia AE cắt (O) tại điểm thứ hai F. a) chứng minh BGDC nội tiếp HELP ME PLEASE

a: Xét ΔAPE và ΔACP có
góc APE=góc ACP
góc PAE chung
=>ΔAPE đồng dạng với ΔACP
=>AP^2=AE*AC=AN^2
Xét ΔAND và ΔABN có
góc AND=góc ABN
góc NAD chung
=>ΔAND đồng dạng với ΔABN
=>AD*AB=AN^2
=>AD*AB=AE*AC
=>AD/AC=AE/ABB
=>ΔADE đồng dạng vơi ΔACB
=>góc ADE=góc ACB
b: góc ADE=góc ACB
=>góc BDE+góc BCE=180 độ
=>BDEC nội tiếp

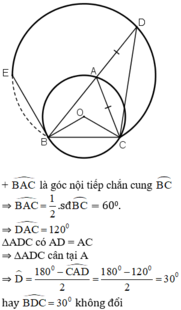
⇒ D nằm trên cung chứa góc 300 dựng trên đoạn BC.
+ Khi A ≡ C thì D ≡ C, khi A ≡ B thì D ≡ E (BE là tiếp tuyến của đường tròn (O) tại B).
Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chứa góc 30º dựng trên BC.

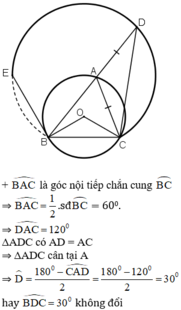
⇒ D nằm trên cung chứa góc 30 ° dựng trên đoạn BC.
+ Khi A ≡ C thì D ≡ C, khi A ≡ B thì D ≡ E (BE là tiếp tuyến của đường tròn (O) tại B).
Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chứa góc 30 ° dựng trên BC.

1)xét tam giác ABC và tam giác HBC có
góc BAC=PHC=90o
đỉnh C chung
=>2 tam giác đồng dạng
=>PH/AB=PC/BC (1)
mà AB =PA (2)
=> tam giác ABC = tam giác ADP ( 2 tam giác vuông có 1 cạnh bằng nhau )
=>BC=PD (3)
từ (1)(2)(3) =>PH/PA=PC/PD=>PA.PC=PH.PD (dpcm)
2) ta có
góc BHP= góc BIC=90o ( chắn nửa hình tròn ) => tứ giác BIDH nội tiếp
=> góc IBH=HCA
=>góc IDP+góc PDC =180o => I,C,D thẳng hàng
CHÚC BẠN HỌC GIỎI
K MÌNH NHÉ
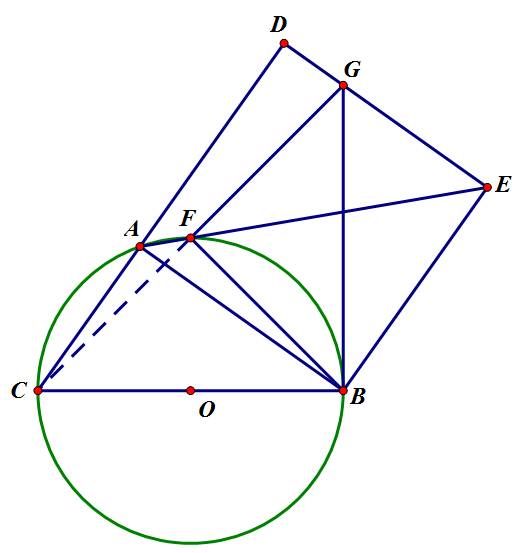
góc GDC=góc GBC=90 => tứ giác nội típ
I là trung điểm của GC
BFC vuông cân niềm tin ak