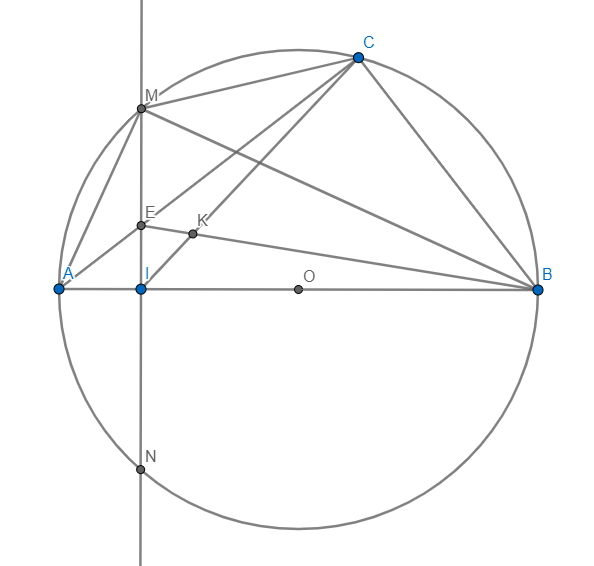
Cho đường tròn (O), một đường kính AB cố định, một điểm I nằm giữa A và O sao cho AI = 1/2.AO (AI = AO/2). Kẻ dây MN vuông góc với AB tại I. Gọi C là điểm tùy ý thuộc cung lớn MN, sao cho C không trùng với M,N và B. Nối AC cắt MN tại E. a) Chứng minh tứ giác IECB nội tiếp được trong đường tròn. b) Chứng minh AM^2 = AE.AC c) Hãy xác định ví trí điểm C sao cho khoảng cách từ N đến tâm đường tròn ngoại tiếp tam giác CME là nhỏ nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ACB=1/2*sđ cung AB=90 độ
góc EIB+góc ECB=180 độ
=>ECBI nội tiếp đường tròn đường kính EB
Tâm là trung điểm của EB
b: Xét ΔANE và ΔACM có
góc ANE=góc ACM(=1/2sđ cung AM)
góc NAE=góc CAM
=>ΔANE đồng dạng với ΔACM

1) Vì AB là đường kính \(\Rightarrow\angle ACB=90\)
\(\Rightarrow\angle ECB+\angle EIB=90+90=180\Rightarrow IECB\) nội tiếp
2)Vì AB là đường kính \(\Rightarrow\angle AMB=90\)
Ta có: \(\angle AME=90-\angle MAB=\angle ABM=\angle ACM\) (ABCM nội tiếp)
Xét \(\Delta AME\) và \(\Delta ACM:\) Ta có: \(\left\{{}\begin{matrix}\angle AME=\angle ACM\\\angle CAMchung\end{matrix}\right.\)
\(\Rightarrow\Delta AME\sim\Delta ACM\left(g-g\right)\)
3) Vì IECB nội tiếp \(\Rightarrow\angle IBK=\angle ECK\)
Xét \(\Delta EKC\) và \(\Delta IKB:\) Ta có: \(\left\{{}\begin{matrix}\angle IKB=\angle EKC\\\angle IBK=\angle ECK\end{matrix}\right.\)
\(\Rightarrow\Delta EKC\sim\Delta IKB\left(g-g\right)\Rightarrow\dfrac{EK}{IK}=\dfrac{EC}{IB}\Rightarrow EK.IB=EC.IK\)

a. ta có:
\(\widehat{EIB}=90\) độ
\(\widehat{ECB}=90\) độ (=\(\widehat{ACB}=90\) độ)
⇒\(\widehat{EIB}+\widehat{ECB}=180\)độ. Vì \(\widehat{EIB}\) và \(\widehat{ECB}\) là hai góc đối diện
⇒ Tứ giác IECB là tứ giác nội tiếp

a: góc ACB=1/2*sđ cung AB=90 độ
góc EIB+góc ECB=180 độ
=>EIBC nội tiếp
b: Sửa đề: AE*AC-AI*AB=0
Xét ΔAIE vuông tại I và ΔACB vuông tại C co
góc IAE chung
=>ΔAIE đồng dạng với ΔACB
=>AI/AC=AE/AB
=>AI*AB=AE*AC
=>AI*AB-AE*AC=0