Cho tam giác ABC vuông tại A. Gọi H là trung điểm của cạnh AC. Trên tia đối của tia HB lấy điểm K sao cho HK=HB. Chứng minh:
a) Tam giác ABH= tam giác CKH
b) KC vuông góc với AC
c) AK song song với BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
Nguyễn Hoàng Minh
1 tháng 1 2022
Đúng(0)
Những câu hỏi liên quan
13 tháng 7 2023
a: Xét ΔABH vuông tại H và ΔKIH vuông tại H có
HA=HK
HB=HI
=>ΔABH=ΔKIH
b: ΔABH=ΔKIH
=>góc ABH=góc KIH
=>AB//IK
c: IK//AB
AB vuông góc AC
=>IK vuông góc AC
=>I,K,E thẳng hàng
d: Xét tứ giác ABKI có
H là trung điểm chung của AK và BI
AK vuông góc BI
=>ABKI là hình thoi
=>AB=AI=IK
=>IK=ID
=>góc IKD=góc IDK
25 tháng 12 2019
Hình tự vẽ nhé !
Giải
a) Xét tam giác MHB và tam giác MKC có
MB = MC ( vì M là trung điểm của BC )
HMB = KMC ( vì đối đỉnh )
MH = MK ( vì m là trung điểm của HK )
Do đó Tam giác MHB = tam giác MKC
26 tháng 11 2016
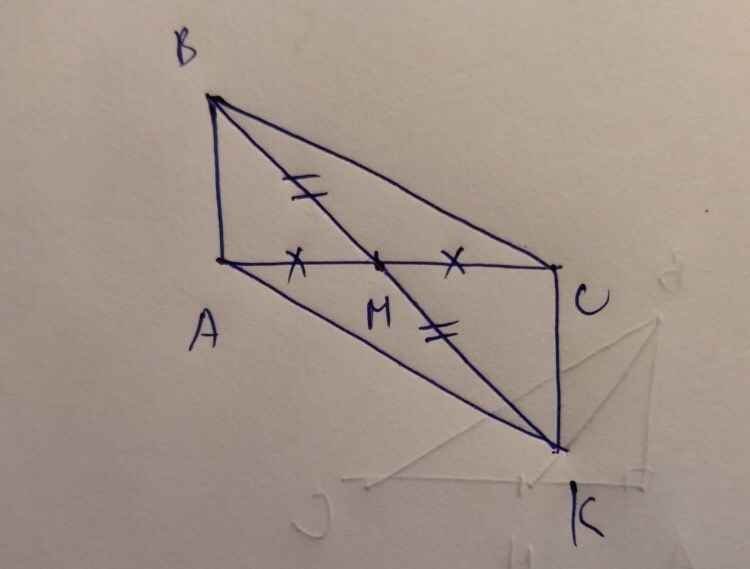
Ta có hình vẽ:
a) Xét Δ ABH và Δ AKH có:
BH = KH (gt)
AHB = AHK = 90o
AH là cạnh chung
Do đó, Δ ABH = Δ AKH (c.g.c) (đpcm)
b) Xét Δ AMK và Δ CME có:
MK = ME (gt)
AMK = CME (đối đỉnh)
AM = CM (gt)
Do đó, Δ AMK = Δ CME (c.g.c)
=> AK = EC (2 cạnh tương ứng) (1)
Δ ABH = Δ AKH (câu a)
=> AB = AK (2 cạnh tương ứng) (2)
Từ (1) và (2) => EC = AB (đpcm)
c) Xét Δ AME và Δ CMK có:
AM = CM (gt)
AME = CMK (đối đỉnh)
ME = MK (gt)
Do đó Δ AME = Δ CMK (c.g.c)
=> AEM = CKM (2 góc tương ứng)
Mà AEM và CKM là 2 góc so le trong nên AE // KC hay AE // BC (đpcm)
26 tháng 11 2016
Giải:
a) Xét \(\Delta ABH,\Delta AKH\) có:
\(BH=HK\left(gt\right)\)
\(\widehat{AHB}=\widehat{AHK}\)
AH: cạnh chung
\(\Rightarrow\Delta ABH=\Delta AKH\left(c-g-c\right)\)
b) Vì \(\Delta ABH=\Delta AKH\)
\(\Rightarrow AB=AK\) ( cạnh tương ứng ) (1)
Xét \(\Delta AMK,\Delta CME\) có:
\(AM=MC\left(=\frac{1}{2}AC\right)\)
\(\widehat{M_1}=\widehat{M_2}\) ( đối đỉnh )
\(EM=KM\left(gt\right)\)
\(\Rightarrow\Delta AMK=\Delta CME\left(c-g-c\right)\)
\(\Rightarrow EC=AK\) ( cạnh tương ứng ) (2)
Từ (1) và (2) \(\Rightarrow EC=AB\left(=AK\right)\)
c) Xét \(\Delta AME\) và \(\Delta CMK\) có:
\(AM=MC\left(=\frac{1}{2}AC\right)\)
\(\widehat{M_3}=\widehat{M_4}\) ( đối đỉnh )
\(KM=EM\left(gt\right)\)
\(\Rightarrow\Delta AME=\Delta CMK\left(c-g-c\right)\)
\(\Rightarrow\widehat{E_1}=\widehat{K_1}\) ( góc tương ứng )
Mà \(\widehat{E_1}\) và \(\widehat{K_1}\) ở vị trí so le trong nên AE // KC hay AE // BC
Vậy a) \(\Delta ABH=\Delta AKH\)
b) EC = AB
c) AE // BC
2
9 tháng 5 2021
xét tam giác ABE và tam giác ADE
AE chung
góc BAE = góc DAE(AE la tia phân giác của góc E)
AB = AD ( gt)
=> tam giác ABE = tam giac DAE ( c.g.c)
b) xét tam giác ABI và tam giác ADI
AI chung
góc BAE = góc DAE
tam giác ABI=tam giác ADI
=> BI = DI ( 2 cạnh t/ứ )
=> I là trung điểm của BD