1x-1y+1z=xyz*7z=?
tìm :x;y;z;?
ai làm được đúng cho tích luôn!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
CM
13 tháng 11 2018
Đ ặ t x = a 3 y = b 3 z = c 3 , v ì x , y , z > 0 x y z = 1 = > a , b , c > 0 a b c = 1
Ta có: x + y + 1 = a 3 + b 3 + 1 = ( a + b ) ( a 2 − a b + b 2 ) + 1 ≥ ( a + b ) a b + 1 = a b ( a + b + c ) = a + b + c c
Do đó: 1 x + y + 1 ≤ c a + b + c
Tương tự ta có: 1 y + z + 1 ≤ a a + b + c 1 z + x + 1 ≤ b a + b + c
Cộng 3 bất đẳng thức trên theo vế ta có đpcm
DA
0
10 tháng 8 2017
2x = 3y suy ra \(\frac{x}{3}\)= \(\frac{y}{2}\) suy ra \(\frac{x}{21}\)= \(\frac{y}{14}\)
5y = 7z suy ra \(\frac{y}{7}\)= \(\frac{z}{5}\)suy ra \(\frac{y}{14}\)= \(\frac{z}{10}\)
Suy ra \(\frac{x}{21}\)= \(\frac{y}{14}\) = \(\frac{z}{10}\) suy ra \(\frac{3x}{63}\) = \(\frac{7y}{98}\)= \(\frac{5z}{50}\) và 3x - 7y + 5z = 30
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{3x}{63}\)= \(\frac{7y}{98}\) = \(\frac{5z}{50}\)= \(\frac{3x-7y+5z}{63-98+50}\) = \(\frac{30}{15}\) = 2
Suy ra x = 3 . 21 = 63
y = 3 . 14 = 42
z = 3 . 10 = 30
Vậy ............................
CM
5 tháng 11 2018
Chọn D.
Phương pháp: Nhận xét rằng ba đường thẳng lần lượt song song với các trục tọa độ và đồng quy tại điểm A(1;-1;0) nên bài toán trở thành bài toán quen thuộc là viết phương trình mặt phẳng đi qua M vuông góc với đường thẳng AM.
NP
0
CM
6 tháng 4 2017
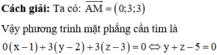
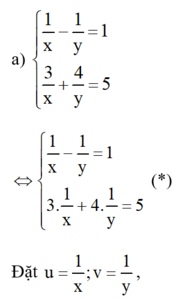
hệ phương trình (*) trở thành :
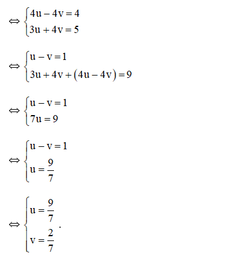
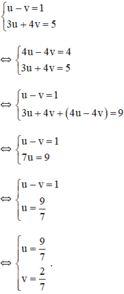
+ u = 9 7 ⇒ 1 x = 9 7 ⇒ x = 7 9 + v = 2 7 ⇒ 1 y − 2 7 ⇒ y − 7 2
Vậy hệ phương trình có nghiệm (7/9;7/2)
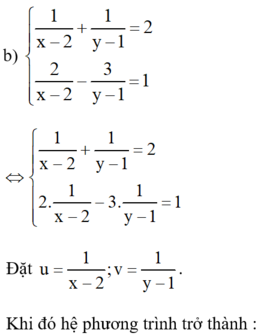
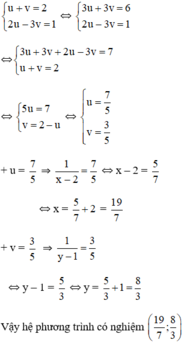
Kiến thức áp dụng
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.
ai tích mk mk tích lai
ai mà trả lời câu hỏi này đầu tiên được nhận 2 tích nha .
trả lời xong tích mk với