A(x)=mx+n
Tìm m,n biết A(1)=3, A(-1)=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 9 2021
a: Để hai đường thẳng song song thì \(\left\{{}\begin{matrix}m-1=1-2m\\n-2\ne n+3\end{matrix}\right.\Leftrightarrow3m=2\Leftrightarrow m=\dfrac{2}{3}\)
b: Để hai đường thẳng cắt nhau thì \(m-1\ne-2m+1\)
\(\Leftrightarrow3m\ne2\)
hay \(m\ne\dfrac{2}{3}\)
NT
Cho A( x ) = x3 + mx + n ( n ; m thuộc Z ). Tìm m và n biết A : ( x - 1 ) dư 4 và A : ( x + 1 ) dư 6
2
22 tháng 10 2019
cách 2 nếu chưa học bezout
x^3 +mx+n x-1 x^2+x+(m+1) x^3-x^2 - x^2+mx+n x^2-x - (m+1)x+n (m+1)x-(m+1) - n+m+1
Mà \(A\left(x\right):\left(x-1\right)\)dư 4\(\Rightarrow m+n+1=4\)
\(\Rightarrow m+n=3\left(1\right)\)
x^3 +mx+n x+1 x^2-x+(m+1) x^3+x^2 - -x^2+mx+n -x^2-x - (m+1)x+n (m+1)x+(m+1) - n-m-1
Mà \(A\left(x\right):\left(x+1\right)\)dư 6\(\Rightarrow n-m-1=6\)
\(\Rightarrow n-m=7\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\Rightarrow\hept{\begin{cases}n+m=3\\n-m=7\end{cases}\Rightarrow\hept{\begin{cases}n=5\\m=-2\end{cases}}}\)
Vậy n=5 và m=-2
22 tháng 10 2019
Áp dụng định lý Bezout ta có:
\(A\left(x\right)\)chia x-1 dư 4 \(\Rightarrow A\left(1\right)=4\)
\(\Rightarrow1+m+n=4\)
\(\Rightarrow m+n=3\left(1\right)\)
\(A\left(x\right)\)chia x+1 dư 6 \(\Rightarrow A\left(-1\right)=6\)
\(\Rightarrow-1-m+n=6\)
\(\Rightarrow-m+n=7\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\Rightarrow\hept{\begin{cases}m+n=3\\-m+n=7\end{cases}\Rightarrow}\hept{\begin{cases}n=5\\m=-2\end{cases}}\)
Vậy n=5 và m=-2
XO
27 tháng 1 2022
a) Ta có f(x) - 5 \(⋮\)x + 1
=> x3 + mx2 + nx + 2 - 5 \(⋮\)x + 1
=> x3 + mx2 + nx - 3 \(⋮\)x + 1
=> x = - 1 là nghiệm đa thức
Khi đó (-1)3 + m(-1)2 + n(-1) - 3 = 0
<=> m - n = 4 (1)
Tương tự ta được f(x) - 8 \(⋮\)x + 2
=> x3 + mx2 + nx - 6 \(⋮\) x + 2
=> x = -2 là nghiệm đa thức
=> (-2)3 + m(-2)2 + n(-2) - 6 = 0
<=> 2m - n = 7 (2)
Từ (1)(2) => HPT \(\left\{{}\begin{matrix}m-n=4\\2m-n=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\n=-1\end{matrix}\right.\)
Vậy đa thức đó là f(x) = x3 + 3x2 - x + 2
XO
27 tháng 1 2022
b) f(x) - 7 \(⋮\)x + 1
=> x3 + mx + n - 7 \(⋮\) x + 1
=> x = -1 là nghiệm đa thức
=> (-1)3 + m(-1) + n - 7 = 0
<=> -m + n = 8 (1)
Tương tự ta được : x3 + mx + n + 5 \(⋮\)x - 3
=> x = 3 là nghiệm đa thức
=> 33 + 3m + n + 5 = 0
<=> 3m + n = -32 (2)
Từ (1)(2) => HPT : \(\left\{{}\begin{matrix}3m+n=-32\\-m+n=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4m=-40\\-m+n=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-10\\n=-2\end{matrix}\right.\)
Vậy f(x) = x3 - 10x -2
2 tháng 9 2021
a: Để hai đường thẳng trùng nhau thì \(\left\{{}\begin{matrix}m-1=1-2m\\n-2=n+3\left(loại\right)\end{matrix}\right.\)
Vậy: Không có (m,n) nào để hai đường thẳng trùng nhau
2 tháng 9 2021
Để hai đường thẳng trùng nhau thì
\(\left\{{}\begin{matrix}m-1=1-2m\\n-2=n+3\left(loại\right)\end{matrix}\right.\)
3 tháng 12 2023
a: Đặt (d1): \(y=\left(2m-1\right)x+n+1\)
(d2): \(y=\left(5-m\right)x-1-n\)
Để (d1) cắt (d2) thì \(2m-1\ne5-m\)
=>\(3m\ne6\)
=>\(m\ne2\)
b: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}2m-1=5-m\\n+1\ne-1-n\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3m=6\\2n\ne-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=2\\n\ne-1\end{matrix}\right.\)
c: Để \(\left(d1\right)\equiv\left(d2\right)\) thì \(\left\{{}\begin{matrix}2m-1=5-m\\n+1=-n-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3m=6\\2n=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=2\\n=-1\end{matrix}\right.\)
LT
0
DT
1
TH
23 tháng 3 2023
+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m . ( - 1 ) 3 + ( m – 2 ) ( - 1 ) 2 – ( 3 n – 5 ) . ( - 1 ) – 4 n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
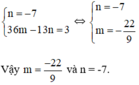
A(1)=3 => m+n=3 => m=3-n
A(-1)=5 => -m+n=5 (1)
Thế m=3-n vào (1) được
-(3-n)+n=5
<=> -3+2n=5
<=> 2n=8
<=> n=4
Thế n=4 vào m=3-n được
m=3-4=-1
=> A(x) -x+4