tìm số hạng tổng quát của cấp số nhân : a. biết tổng bằng 32 và u2=8
b. biết tổng =5/3 và tổng thứ 3 số hạng đầu tiên bằng 39/25
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số đầu là x.
Cấp số cộng là q.
=> Số đầu, thứ 2. 3,4,5 là x,x+q,x+2q,x+3q,x+4q.
Tổng số 1 và 3 là x + (x+2q) = 28
Tổng số 3 và cuối là (x+2q)+(x+4q)=40.
Ta đã có 2 phương trình tạo thành 1 hệ phương trình.
Giải hệ tìm x và q.
Chúc em học tốt!

Chọn đáp án B
Giả sử cấp số cộng có số hạng đầu là u 1 và công sai d.
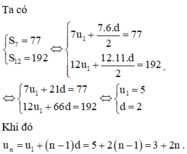

Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
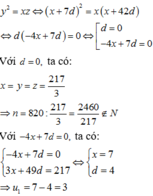
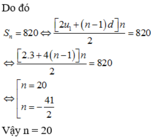
Bạn kiểm tra lại đề bài, phải là csn lùi vô hạn thì mới tính được
a/ \(S=\dfrac{u_1}{1-q}=32;u_2=u_1.q=8\)
\(\Rightarrow\dfrac{\dfrac{8}{q}}{1-q}=32\Leftrightarrow q=\dfrac{1}{2}\Rightarrow u_1=\dfrac{8}{\dfrac{1}{2}}=16\)
\(\Rightarrow u_n=16.\left(\dfrac{1}{2}\right)^{n-1}=32.\left(\dfrac{1}{2}\right)^n\)
b/ \(S_3=u_1+u_2+u_3=\dfrac{39}{25};S=\dfrac{u_1}{1-q}=\dfrac{5}{3}\)
\(S_3=u_1+u_1.q+u_1q^2=\dfrac{39}{25}\Leftrightarrow u_1\left(1+q+q^2\right)=\dfrac{39}{25}\)
\(\Rightarrow u_1=\dfrac{39}{25\left(1+q+q^2\right)}\Rightarrow\dfrac{\dfrac{39}{25\left(1+q+q^2\right)}}{1-q}=\dfrac{5}{3}\)
\(\Leftrightarrow q=...\Rightarrow u_1=...\Rightarrow u_n=u_1.q^{n-1}\)
P/s: Bạn tự làm nốt ạ