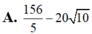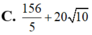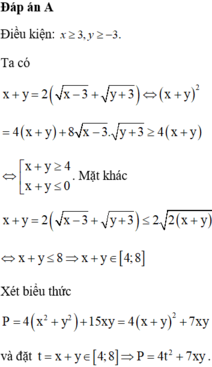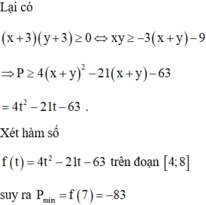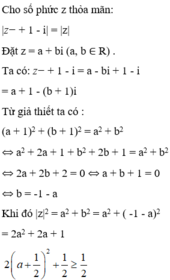cho hai số thực m,n khác 0 thay đổi thỏa mãn đk: ( m+n)mn=m^2+n^2. Giá trị nhỏ nhất của bt A= 1/m^3+1/n^3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
22 tháng 11 2021
\(a+b=1\Leftrightarrow b=1-a\\ \Leftrightarrow P=a^2+1-a=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ P_{min}=\dfrac{3}{4}\Leftrightarrow a=\dfrac{1}{2}\Leftrightarrow b=\dfrac{1}{2}\)
T
18 tháng 8 2019
a) Từ đề bài có: \(x\left(x-1\right)\le0\Rightarrow x^2\le x\)
Tương tự hai BĐT còn lại và cộng theo vế suy ra:
\(M=x+y+z-3\ge x^2+y^2+z^2-3=-2\)
Đẳng thức xảy ra khi (x;y;z) = (0;0;1) và các hoán vị của nó
Is it true?
18 tháng 8 2019
\(4\le\sqrt{x}+\sqrt{y}+\sqrt{xy}+1\le\sqrt{2\left(x+y\right)}+\frac{x+y}{2}+1\)
\(\Leftrightarrow\)\(8\le x+y+2\sqrt{x+y}\sqrt{2}+2=\left(\sqrt{x+y}+\sqrt{2}\right)^2\)
\(\Leftrightarrow\)\(\sqrt{x+y}+\sqrt{2}\ge\sqrt{8}\)
\(\Leftrightarrow\)\(x+y\ge\left(\sqrt{8}-\sqrt{2}\right)^2=2\)
\(\Rightarrow\)\(P=\frac{x^2}{y}+\frac{y^2}{x}\ge\frac{\left(x+y\right)^2}{x+y}=x+y\ge2\)
Dấu "=" xảy ra khi \(x=y=1\)
6 tháng 2 2019
Đề là tìm GTLN chứ nhỉ ?
Ta có : \(5x^2+8xy+5y^2=36\)
\(\Leftrightarrow x^2+y^2+4\left(x^2+2xy+y^2\right)=36\)
\(\Leftrightarrow M+4\left(x+y\right)^2=36\)
\(\Leftrightarrow M=36-4\left(x+y\right)^2\le36\)
Dấu ''=" khi x = -y
Thế vào pt ban đầu sẽ tìm đc giá trị cụ thể của x ; y
