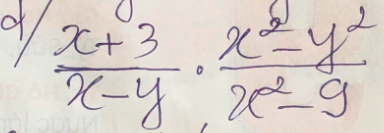
ai giúp mik đc ko
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TL
1
26 tháng 12 2021
bạn phải đặng nhập víp mứi được
cơ ok nha
bạn chỉ sử dụng 3 lần miễn phí thôi''
ok nha
hok tốt
sao mik đăng lên mà ko ai giúp vậy?ai xem đc giúp mik với...
ND
9
NN
11
CN
0
11 tháng 1 2023
Bài 3:
a: \(=\dfrac{x-2+x}{2x-4}=\dfrac{2x-2}{2x-4}=\dfrac{x-1}{x-2}\)
b: \(=\dfrac{6}{5\left(x-4\right)}-\dfrac{x-5}{\left(x-4\right)^2}\)
\(=\dfrac{6x-24-5x+25}{5\left(x-4\right)^2}=\dfrac{x+1}{5\left(x-4\right)^2}\)
c: \(=\dfrac{3x+2-12x+8+3x-6}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{-6x+4}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{-2}{3x+2}\)
10 tháng 9 2023
5:
a: \(\Leftrightarrow A-B+2xy^2-x^2y=3x^2y\)
=>\(A-B=3x^2y+x^2y-2xy^2=4x^2y-2xy^2\)
b: \(\Leftrightarrow A-B-\dfrac{3}{8}xy^2=\dfrac{3}{4}xy^2-\dfrac{1}{2}xy^2=\dfrac{1}{4}xy^2\)
=>\(A-B=\dfrac{1}{4}xy^2+\dfrac{3}{8}xy^2=\dfrac{5}{8}xy^2\)
c: \(\Leftrightarrow-2x^2y^3-\left(A-B\right)=8x^3y^2\)
=>\(A-B=-2x^2y^3-8x^3y^2\)
1 tháng 10 2023
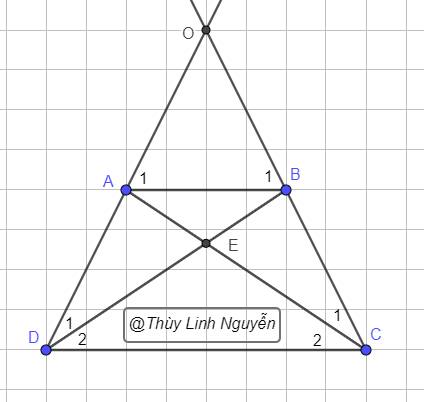
`a,`
Có `AB////CD(g t)`
`=>{(hat(A_1)=hat(ADC)(Sol etrong)),(hat(B_1)=hat(BCD)(Sol etrong)):}`
Mà `hat(ADC)=hat(BCD)` (Tứ giác `ABCD` là hình thang cân)
Nên `hat(A_1)=hat(B_1)`
`=>Delta OAB` cân tại `O(dpcm)`
`b,`
Tứ giác `ABCD` là hình thang cân `(g t)`
`=>hat(BAD)=hat(ABC);AD=BC`
Xét `Delta ABD` và `Delta BAC` có :
`{:(AB-chung),(hat(BAD)=hat(BAC)(cmt)),(AD=BC(cmt)):}}`
`=>Delta ABD=Delta BAC(c.g.c)(dpcm)`
`c,`
Có `Delta ABD=Delta BAC(cmt)`
`=>hat(D_1)=hat(C_1)` (2 góc tương ứng)
mà `hat(ADC)=hat(BCD)(cmt)`
Nên `hat(ADC)-hat(D_1)=hat(BCD)-hat(C_1)`
hay `hat(D_2)=hat(C_2)`
`=>Delta EDC` cân tại `E`
`=>ED=EC(dpcm)`
Hình:
\(\dfrac{x+3}{x-y}.\dfrac{x^2-y^2}{x^2-9}=\dfrac{x+3}{x-y}.\dfrac{\left(x-y\right)\left(x+y\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{x+y}{x-3}\)