Giải phương trình nghiệm nguyên
x2 + y2 = 3 - xy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 7 2021
\(x+y+xy=x^2+y^2\)
⇔ \(2xy+2x+2y=2x^2+2y^2\)
⇔ \(\left(x^2+y^2-2xy\right)+\left(x^2-2x+1\right)+\left(y^2-2y+1\right)=2\)
⇔ \(\left(x-y\right)^2+\left(x-1\right)^2+\left(y-1\right)^2=2\)
⇔ 
⇔ 
Các cặp số nguyên (x, y) thỏa mãn phương trình là : (0; 0); (2; 2); (0; 1); (2; 1); (1; 0);(1;2).
CM
26 tháng 7 2019
Ta có x + y 2 + y = 3 2 x 2 + y 2 + x y + x = 5 ⇔ 2 x 2 + 4 x y + 2 y 2 + 2 y = 6 2 x 2 + 2 y 2 + 2 x y + x = 5
Suy ra 2xy + 2y – x – 1 = 0 ⇔ (x + 1) (2y – 1) = 0 ⇔ x = −1 hoặc y = 1 2
Với x = −1, ta được y 2 – y – 2 = 0 ⇔ y = − 1 y = 2
Ta được hai nghiệm (−1; −1) và (−1; 2)
Với y = 1 2 , ta được x 2 + x − 9 4 = 0 ⇔ x = − 1 ± 10 2
Ta được hai nghiệm − 1 − 10 2 ; 1 2 và − 1 + 10 2 ; 1 2
Vậy hệ có bốn nghiệm (−1; −1); (−1; 2); − 1 − 10 2 ; 1 2 và − 1 + 10 2 ; 1 2
Đáp án:A
NH
1
CM
13 tháng 4 2019
Phương trình 1 ⇔ x + y 2 x - y = 0 ⇔ x = − y 2 x = y
Trường hợp 1: x = - y thay vào (2) ta được x 2 - 4 x + 3 = 0 ⇔ x = 1 x = 3
Suy ra hệ phương trình có hai nghiệm là (1; −1), (3; −3).
Trường hợp 2: 2 x = y thay vào (2) ta được - 5 x 2 + 17 x + 3 = 0 phương trình này không có nghiệm nguyên.
Vậy các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là (1; −1) và (3; −3).
Đáp án cần chọn là: C
NN
1
PT
1
CM
27 tháng 4 2019
Nhận thấy x = y = 0 không là nghiệm của hệ phương trình đã cho nên ta có:
x y = 96 x 2 + y 2 = 208 ⇔ x = 96 y 9216 y 2 + y 2 = 208 ⇔ x = 96 y y 4 − 208 y 2 + 9216 = 0
⇔ x = 96 y y 2 − 144 y 2 − 144 = 0 ⇔ x = 96 y y = ± 8 y = ± 12 ⇔ y = − 12 ; x = − 8 y = 12 ; x = 8 y = 8 ; x = 12 y = − 8 ; x = − 12
Vậy hệ đã cho có bốn nghiệm
Đáp án cần chọn là: A
CM
14 tháng 4 2018
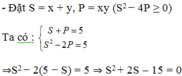
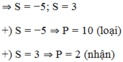
Khi đó: x, y là nghiệm của phương trình X 2 - 3 X + 2 = 0 ⇔ X = 1 ; X = 2
Vậy hệ có nghiệm (2; 1), (1; 2)
Đáp án cần chọn là: C
PT
1
x=1
y=1