Tìm nghiệm dương của phương trình x2-2y2=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 11 2021
Lời giải:
$x^2-2y^2=5\Rightarrow x$ lẻ. Đặt $x=2k+1$ với $k$ nguyên
$x^2-2y^2=5$
$\Leftrightarrow (2k+1)^2-2y^2=5$
$\Leftrightarrow 2k^2+2k-y^2=2$
$\Rightarrow y$ chẵn. Đặt $y=2t$ với $t$ nguyên
PT trở thành: $2k^2+2k-4t^2=2$
$\Leftrightarrow k^2+k-2t^2=1$
Điều này vô lý do $k^2+k-2t^2=k(k+1)-2t^2$ chẵn còn $1$ thì lẻ
Vậy pt vô nghiệm.
9 tháng 1 2021
Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).
Vậy pt vô nghiệm nguyên.
9 tháng 1 2021
2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).
CM
20 tháng 5 2019
Đáp án: D
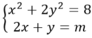
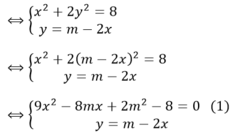
Để hệ phương trình có nghiệm thì phương trình (1) có nghiệm, tức là:
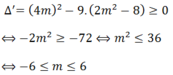
Vậy giá trị lớn nhất của m để hệ phương trình có nghiệm là 6.
DV
1
AH
Akai Haruma
Giáo viên
27 tháng 12 2021
Lời giải:
PT $\Leftrightarrow x^2+x(3y-1)+(2y^2-2)=0$
Coi đây là pt bậc 2 ẩn $x$ thì:
$\Delta=(3y-1)^2-4(2y^2-2)=y^2-6y+9=(y-3)^2$. Do đó pt có 2 nghiệm:
$x_1=\frac{1-3y+y-3}{2}=-y-1$
$x_2=\frac{1-3y+3-y}{2}=2-2y$
Đến đây bạn thay vô pt ban đầu để giải pt bậc 2 một ẩn thui.
CM
24 tháng 7 2019
Ta có 2 x + y = 5 m − 1 x − 2 y = 2
⇔ y = 5 m − 1 − 2 x x − 2 5 m − 1 − 2 x = 2 ⇔ y = 5 m − 1 − 2 x 5 x = 10 m
⇔ x = 2 m y = m − 1
Thay vào x 2 – 2 y 2 = − 2 ta có
x 2 – 2 y 2 = − 2 ⇔ ( 2 m 2 ) – 2 ( m − 1 ) 2 = − 2 ⇔ 2 m 2 + 4 m = 0 ⇔ m = 0 m = − 2
Vậy m ∈ {−2; 0}
Đáp án: C
CM
25 tháng 3 2018
Ta có
2 x + 3 y = 7 2 − m 4 x − y = 5 m ⇔ 4 x + 6 y = 7 − 2 m 4 x − y = 5 m ⇔ 7 y = 7 − 7 m 4 x − y = 5 m ⇔ y = 1 − m 4 x − 1 − m = 5 m ⇔ y = 1 − m x = 4 m + 1 4
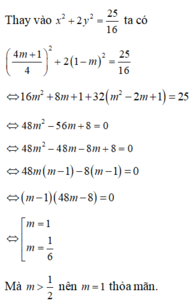
Đáp án: B
CM
25 tháng 1 2018
Đặt t = f ( x ) = x 2 - 4 x + 5 .
ta có f ' ( x ) = x - 2 x 2 - 4 x + 5 và f ' = 0 ⇔ x = 2
Xét x> 0 ta có bảng biến thiên
Khi đó phương trình đã cho trở thành m= t2+ t- 5hay t2+ t- 5-m= 0 (*)
Nếu phương trình (* ) có nghiệm t1; t2 thì t1+ t2= -1.
Do đó (*) có nhiều nhất 1 nghiệ m t ≥ 1.
Vậy phương trình đã cho có đúng 2 nghiệm dương khi và chỉ khi phương trình (*) có đúng 1 nghiệm t ∈ (1; √5).
+ Đặt g(t) = t2+ t- 5. Ta đi tìm m để phương trình (*) có đúng 1 nghiệm t ∈ (1; √5).
Ta có g’(t) = 2t + 1 > 0, ∀ t ∈ (1; √5).
Bảng biến thiên:
Từ bảng biến thiên suy ra là các giá trị cần tìm.
Chọn B.