Tìm GTNN help cần gấp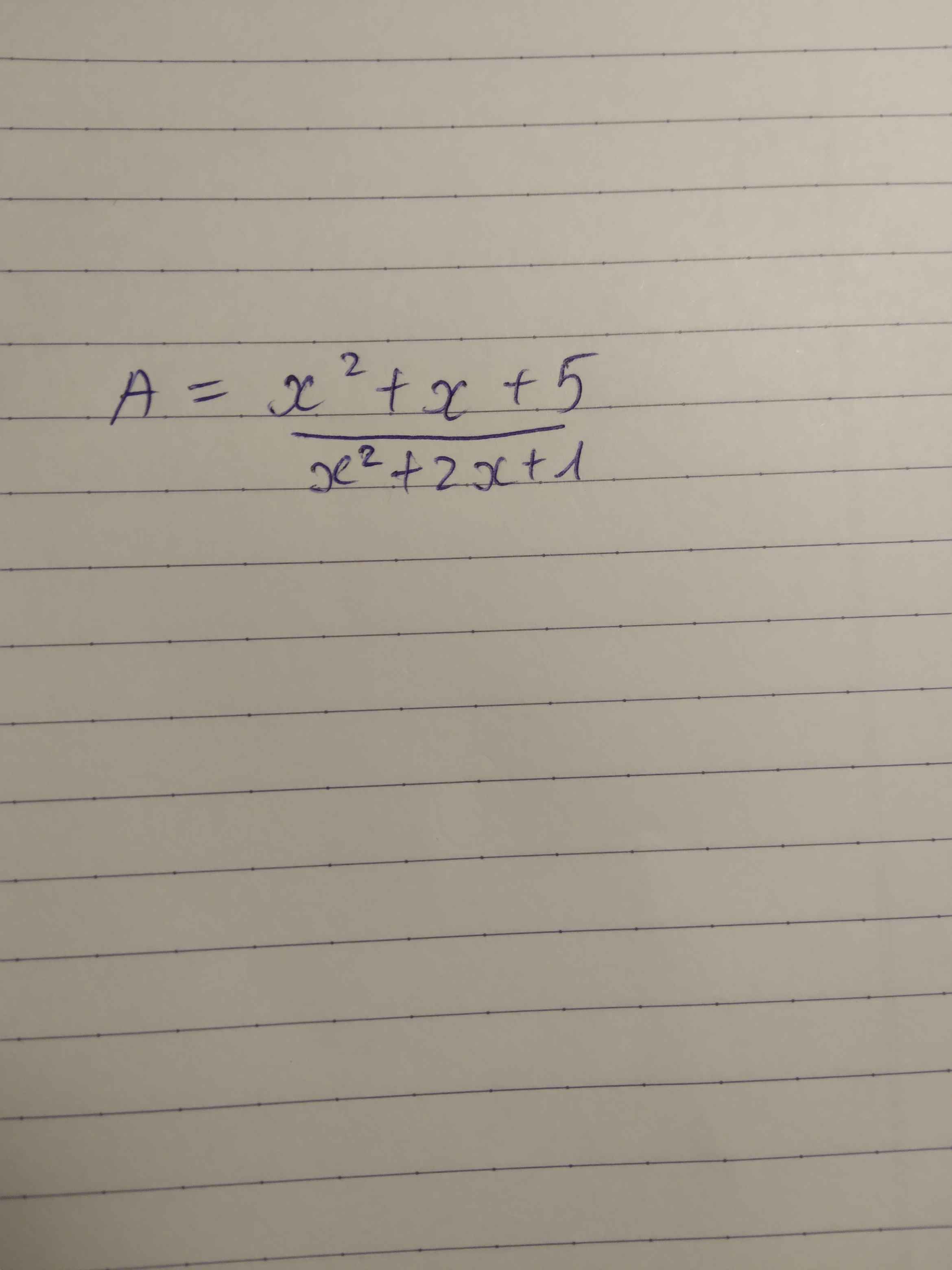
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐK:\(x\ge2\)
\(A=x-2\sqrt{x-2}+3=x-2-2\sqrt{x-2}+1+4=\left(\sqrt{x-2}-1\right)^2+4\)Mà ta có \(\left(\sqrt{x-2}-1\right)^2\ge0\)\(\Leftrightarrow\)\(\left(\sqrt{x-2}-1\right)^2+4\ge4\Leftrightarrow A\ge4\)
Dấu bằng xảy ra khi \(\sqrt{x-2}-1=0\Leftrightarrow\sqrt{x-2}=1\Leftrightarrow x-2=1\Leftrightarrow x=3\)
Vậy GTNN của A là 4
Đây là cách làm của mình thôi, không biết có đúng không.
A = x - 2 \(\sqrt{x}\)- 2+3
= x \(-2\sqrt{x}+1\)
= \((\sqrt{x}-1)^2\)
Mà \((\sqrt{x}-1)^2\ge0\)
=> A \(\ge0\)
Vậy GTNN của A là 0 khi x = 1

\(A=x^2-12x+7=x^2-12x+36-29\)
\(=\left(x-6\right)^2-29\ge-29\)
Vậy \(A_{min}=-29\Leftrightarrow x=6\)
\(C=x-x^2-4=-\left(x^2-x+4\right)\)
\(=-\left(x^2-x+\frac{1}{4}+\frac{3}{4}\right)\)
\(=-\left[\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\right]\)
\(=-\left[\left(x-\frac{1}{2}\right)^2\right]-\frac{3}{4}\le-\frac{3}{4}\)
Vậy \(C_{min}=\frac{-3}{4}\Leftrightarrow x=\frac{1}{2}\)

\(A=x^2-4xy+7y^2+10x-24y+30\\ =\left(x^2-4xy+4y^2\right)+10\left(x-y\right)+25+\left(3y^2-14y+\dfrac{49}{3}\right)-\dfrac{34}{3}\\ =\left(x-2y+5\right)^2+3\left(y-\dfrac{7}{3}\right)^2-\dfrac{34}{5}\)
Với mọi x;y thì \(\left(x-2y+5\right)^2\ge0;3\left(y-\dfrac{7}{3}\right)^2\ge0\)
Do đó:\(A\ge-\dfrac{34}{5}\)
Để \(A=-\dfrac{34}{5}\) thì:
\(\left[{}\begin{matrix}\left(x-2y+5\right)^2=0\\\left(y-\dfrac{7}{3}\right)^2=0\\\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2y=-5\\y=\dfrac{7}{3}\\\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5+\dfrac{2.7}{3}=-\dfrac{1}{3}\\y=\dfrac{7}{3}\\\end{matrix}\right.\)
Vậy...
Nguyễn Thị Hồng Nhung, Akai Haruma, Trần Hoàng Nghĩa, Trần Thiên Kim, Phạm Hoàng Giang, Nhật Hạ, DƯƠNG PHAN KHÁNH DƯƠNG, Toshiro Kiyoshi, Ribi Nkok Ngok, ...


a) Ta có: \(A=\left(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right):\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
b) Thay \(x=7+4\sqrt{3}\) vào A, ta được:
\(A=\dfrac{2+\sqrt{3}+2}{2+\sqrt{3}-2}=\dfrac{4+\sqrt{3}}{\sqrt{3}}=\dfrac{4\sqrt{3}+3}{3}\)
c) Ta có: \(M=\dfrac{x+5}{\sqrt{x}-2}:\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
\(=\dfrac{x+5}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
\(=\dfrac{x+5}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}-4\)
\(\Leftrightarrow M\ge2\cdot\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{9}{\sqrt{x}+2}}-4\)
\(\Leftrightarrow M\ge2\cdot3-4=6-4=2\)
Dấu '=' xảy ra khi \(\sqrt{x}+2=3\)
\(\Leftrightarrow\sqrt{x}=1\)
hay x=1

a, Vì |x-3| \(\ge\)0
=>A=|x-3|+50\(\ge\)50
Dấu "=" xảy ra khi x=3
Vậy GTNN của A = 50 khi x=3
b, Vì |x+8| \(\ge0\)
=>B=2014-|x+8|\(\le2014\)
Dấu "=" xảy ra khi x=-8
Vậy GTLN của B = 2014 khi x=-8
c, Vì \(\hept{\begin{cases}\left|x-100\right|\ge0\\\left|y+2014\right|\ge0\end{cases}}\)
\(\Rightarrow\left|x-100\right|+\left|y+2014\right|\ge0\)
\(\Rightarrow C=\left|x-100\right|+\left|y+2014\right|-2015\ge-2015\)
Dấu "=" xảy ra khi x=100,y=-2014
Vậy GTNN của C=-2015 khi x=100,y=-2014
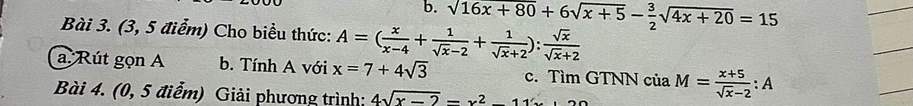 mn giúp em phần tìm gtnn vs ạ, em cần gấp
mn giúp em phần tìm gtnn vs ạ, em cần gấp
\(A=\dfrac{x^2+x+5}{\left(x+1\right)^2}\)
Đặt \(x+1=t\Rightarrow x=t-1\)
\(\Rightarrow A=\dfrac{\left(t-1\right)^2+t-1+5}{t^2}=\dfrac{t^2-t+5}{t^2}=\dfrac{5}{t^2}-\dfrac{1}{t}+1=5\left(\dfrac{1}{t}-\dfrac{1}{10}\right)^2+\dfrac{19}{20}\ge\dfrac{19}{20}\)
\(A_{min}=\dfrac{19}{20}\) khi \(t=10\) hay \(x=9\)