Giúp mình với. Cảm ơn nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Chu vi là \(\left(12+5\right).2=34\left(m\right)\)
Diện tích là \(12.5=60\left(m^2\right)=600000\left(cm^2\right)\)
b. Cần lát \(600000:\left(40.40\right)=375\) viên gạch

Xét phương trình phần đường bao:
\(\left(x+3\right)^2+\left(y+1\right)^2=1\Leftrightarrow\left(y+1\right)^2=1-\left(x+3\right)^2\)
\(\Leftrightarrow y+1=\pm\sqrt{1-\left(x+3\right)^2}\) (với \(-4\le x\le-2\))
\(\Leftrightarrow y=-1\pm\sqrt{1-\left(x+3\right)^2}\)
\(V=\pi\int\limits^{-2}_{-4}\left[\left(-1-\sqrt{1-\left(x+3\right)^2}\right)^2-\left(-1+\sqrt{1-\left(x+3\right)^2}\right)^2\right]dx\)
\(=\pi\int\limits^{-2}_{-4}4\sqrt{1-\left(x+3\right)^2}dx\)
Đặt \(x+3=sint\Rightarrow dx=cost.dt\) ; \(\left\{{}\begin{matrix}x=-4\Rightarrow t=-\dfrac{\pi}{2}\\x=-2\Rightarrow t=\dfrac{\pi}{2}\end{matrix}\right.\)
\(V=\pi\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}4cost.cost.dt=2\pi\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\left(1+cos2t\right)=\pi\left(t+\dfrac{1}{2}sin2t\right)|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}=2\pi^2\)
Có vẻ cả 4 đáp án đều không chính xác



a: Theo đề, ta có:
BH+CH=25(cm)
hay BH=25-CH
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC\left(HC-25\right)=-144\)
\(\Leftrightarrow HC=16\left(cm\right)\)
\(\Leftrightarrow HB=9\left(cm\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{9\cdot25}=15\left(cm\right)\\AC=\sqrt{16\cdot25}=20\left(cm\right)\end{matrix}\right.\)

a, \(A=\left(\dfrac{8}{3}xy^2\right).\left(\dfrac{-1}{4}x^2y^5\right).\left(10x^5y^7\right)^0\)
⇒\(A=\dfrac{8}{3}xy^2.\dfrac{-1}{4}x^2y^5.1\)
⇒\(A=\left(\dfrac{8}{3}.\dfrac{-1}{4}.1\right).\left(x.x^2\right).\left(y^2.y^5\right)\)
⇒\(A=\dfrac{-2}{3}x^3y^7\)
+)Hệ số: \(\dfrac{-2}{3}\)
+)Bậc:10
b, Thay \(x=2\), \(y=-1\) vào A ta có:
\(A=\dfrac{-2}{3}.2^3.\left(-1\right)^7\)
⇒\(A=\dfrac{-2}{3}.8.\left(-1\right)\)
⇒\(A=\dfrac{16}{3}\)
Vậy \(A=\dfrac{16}{3}\) khi \(x=2,y=-1\)

uses crt;
var n,i:integer;
begin
clrscr;
readln(n);
for i:=1 to n do
if (n mod i=0) and (i%2=1) then write(i:4);
readln;
end.

Bài 22:
a. Sai. Hình thoi có 4 cạnh bằng nhau
b. Sai.Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.
c. Đúng
d. Đúng
e. Sai. Không phải hình nào cũng có trục đối xứng.
f. Đúng
g. Đúng
i. Sai. Hình chữ nhật có hai đường chéo bằng nhau
k. Sai. Hình lục giác có 3 đường chéo chính.
l. Sai. Hình lúc giác đều có 6 cạnh bằng nhau, 6 góc ở đỉnh bằng nhau.
Bài 23:
a. Khi chiều rộng bằng chiều dài, thì mảnh đất trở thành hình vuông có độ dài cạnh 10 m
Diện tích mảnh đất trồng lạc: $10\times 10=100$ (m2)
b. Chiều dài của bờ rào là:
$2\times (10+10)=40$ (m)





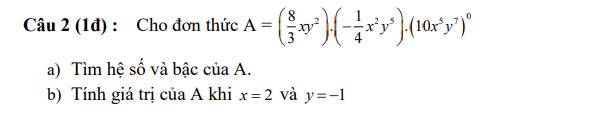 giúp mình với, mình cảm ơn nhiều
giúp mình với, mình cảm ơn nhiều



\(B=\frac{1}{\sqrt{x}+3}-\frac{\sqrt{x}+1}{3-\sqrt{x}}-\frac{2\sqrt{x}}{x-9}\)
\(=\frac{\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\frac{2\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{\sqrt{x}-3+x+4\sqrt{x}+3-2\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\frac{x+3\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\frac{\sqrt{x}}{\sqrt{x}-3}\).