2. Tìm số nguyên x,y biết: x(y + 1) - 3y = 18
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
0
XO
25 tháng 7 2020
Ta có : 2x + xy - 3y = 18
=> x(y + 2) - 3y = 18
=> x(y + 2) - 3y - 6 = 18 - 6
=> x(y + 2) - 3(x + 2) = 12
=> (x - 3)(y + 2) = 12
Vì \(x;y\inℤ\Rightarrow\hept{\begin{cases}x-3\inℤ\\y+2\inℤ\end{cases}}\)
Lại có : 12 = 1.12 = 3.4 = 2.6 = (-1).(-12) = (-3).(-4) = (-2).(-6)
Lập bảng xét 12 trường hợp
| x - 3 | 1 | 12 | -1 | -12 | 3 | 4 | -3 | -4 | 2 | 6 | -2 | -6 |
| y + 2 | 12 | 1 | -12 | -1 | 4 | 3 | -4 | -3 | 6 | 2 | -6 | -2 |
| x | 4 | 15 | 2 | -9 | 6 | 7 | 0 | -1 | 5 | 9 | 1 | -3 |
| y | 10 | -1 | -14 | -3 | 2 | 1 | -6 | -5 | 4 | 0 | -8 | -4 |
Vậy các cặp số (x;y) nguyên thỏa mãn là : (4 ; 10) ; (15 ; - 1) ; (2 ; -14) ; (-9 ; -3) ; (6 ; 2) ; (7 ; 1) ; (0 ; -6) ; (-1 ' 5) ; (5 ; 4) ; (9 ; 0) ;
(1 ; -8) ; (-3 ; -4)
b) \(\left(x^2-5\right)\left(x^2-25\right)< 0\)
TH1 : \(\hept{\begin{cases}x^2-5>0\\x^2-25< 0\end{cases}\Rightarrow\hept{\begin{cases}x^2>5\\x^2< 25\end{cases}}\Rightarrow5< x^2< 25\Rightarrow x^2\in\left\{9;16\right\}}\)(vì x là số nguyên)
=> \(x\in\left\{\pm3;\pm4\right\}\)
TH2 : \(\hept{\begin{cases}x^2-5< 0\\x^2-25>0\end{cases}}\Rightarrow\hept{\begin{cases}x^2< 5\\x^2>25\end{cases}}\Rightarrow x\in\varnothing\)
Vậy \(x\in\left\{\pm3;\pm4\right\}\)
25 tháng 7 2020
2x + xy - 3y = 18
<=> 2x + xy - 6 - 3y = 12
<=> ( 2x + xy ) - ( 6 + 3y ) = 12
<=> x( 2 + y ) - 3( 2 + y ) = 12
<=> ( x - 3 )( 2 + y ) = 12
Lập bảng :
| x-3 | 1 | -1 | 2 | -2 | 3 | -3 | 4 | -4 | 6 | -6 | 12 | -12 |
| x | 4 | 2 | 5 | 1 | 6 | 0 | 7 | -1 | 9 | -3 | 15 | -9 |
| 2+y | 12 | -12 | 6 | -6 | 4 | -4 | 3 | -3 | 2 | -2 | 1 | -1 |
| y | 10 | -14 | 4 | -8 | 2 | -6 | 1 | -5 | 0 | -4 | -1 | -3 |
Vậy ta có 12 cặp ( x ; y ) thỏa mãn
( 4 ; 10 ) , ( 2 ; -14 ) , ( 5 ; 4 ) , ( 1 ; -8 ) , ( 6 ; 2 ) , ( 0 ; -6 ) , ( 7 ; 1 ) , ( -1 ; -5 ) , ( 9 ; 0 ) , ( -3 ; -4 ) , ( 15 ; -1 ) , ( -9 ; -3 )
XO
8 tháng 6 2021
y2 + 3y = x4 + x2 + 18
<=> 4y2 + 12y = 4x4 + 4x2 + 72
<=> 4y2 + 12y + 9 = 4x4 + 4x2 + 1 + 80
<=> (2y + 3)2 = (2x2 + 1)2 = 80
<=> (2x2 + 1 + 2y + 3)(2y + 3 - 2x2 - 1) = 80
<=> (2x2 + 2y + 4)(-2x2 + 2y + 2) = 80
<=> (x2 + y + 2)(-x2 + y + 1) = 20
Lập bảng xét các trường hợp
| x2 + y + 2 | 1 | 20 | -20 | -1 | 4 | 5 | -5 | -4 | 2 | 10 | -2 | -10 |
| -x2 + y + 1 | 20 | 1 | -1 | -20 | 5 | 4 | -4 | -5 | 10 | 2 | -10 | -2 |
| x | | | \(\pm3\) | | | \(\pm3\) | | | 0 | | | 0 | ||||
| y | 9 | 9 | -12 | -12 | 3 | 3 | -6 | -6 | | | | | | | | |
Vậy các cặp (x;y) thỏa mãn là (-3 ; 9) ; (3;9) ; (-3 ; -12) ; (3;-12) ; (0;3) ; (0;-6)
KS
1
29 tháng 3 2020
+) Xét \(x=0\)
\(\Rightarrow\left(3y+1\right)\left(y+1\right)=21\)
\(\Rightarrow3y+1;y+1\inƯ\left(21\right)=\left\{\pm1;\pm3;\pm7;\pm21\right\}\)
Mà \(3y+1\) chia \(3\) dư \(1;-2\)
\(\Rightarrow3y+1\in\left\{1;-2;7\right\}\)
\(\Rightarrow y\in\left\{0;-1;2\right\}\)
+) Với \(y=0\)
\(\Rightarrow y+1=1\) ( loại )
+) Với \(y=-1\)
\(\Rightarrow y+1=0\) ( loại )
+) Với \(y=2\)
\(\Rightarrow y+1=3\) ( thỏa mãn )
+) Xét \(x\ne0\)
\(\Rightarrow2^{\left|x\right|}+x\left(x+1\right)\) chẵn
\(\Rightarrow y\) lẻ
\(\Rightarrow2x+3y+1\) chẵn
Mà \(21\) lẻ
\(\Rightarrow x\ne0\) phương trình vô nghiệm
Vậy \(\left(x;y\right)=\left(0;2\right)\)
DV
2
DA
2 tháng 3 2020
(2x+1) . (3y -2)=-5
=> 2x+1 \(\in\)Ư(-5) = { 1; 5; -1; -5}
=> 2x \(\in\){ 0; 6; -2; -6}
=> x \(\in\){ 0; 3; -1; -3}
Sau bn tự thay nha
2 tháng 3 2020
\(\left(2x+1\right)\left(3y-2\right)=5\)
Do x,y nguyên => 2x+1; 3y-2 nguyên
=> 2x+1; 3y-2\(\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\)
| 2x+1 | -5 | -1 | 1 | 5 |
| 3y-2 | -1 | -5 | 5 | 1 |
| x | -3 | -1 | 0 | 2 |
| y | \(\frac{1}{3}\) | -1 | \(\frac{7}{3}\) | 1 |
Vậy (x;y)=(-1;-1);(2;1)
PT
1
PT
1
CM
23 tháng 3 2017
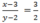nên 2(x – 3) = 3(y – 2)
Do đó 2x – 6 = 3y – 6 nên 2x = 3y
Suy ra 2x – 2y = y hay 2(x – y) = y
Nên 2.4 = y
Vậy y = 8, x = 3y / 2 = 3.8 /2 = 12