cho tam giác ABC vuông tại A. K là trung điểm của BC dựng đường thẳng d vuông góc với AK, d cắt AB tại D và cắt AC tại E. lấy I là trung điểm của DE.
a)chứng minh AI vuông góc với BC
b)có thể nói DE<BC không tại sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
6 tháng 3 2018
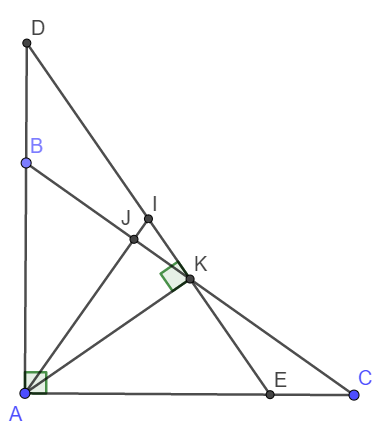
a) Xét tam giác vuông ABC có K là trung điểm nên theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có: KB = KA
Hay tam giác KAB cân tại K, suy ra \(\widehat{KBA}=\widehat{KAB}\)
Xét tam giác vuông ADE có I là trung điểm nên theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông, ta có: ID = IA
Hay tam giác IDA cân tại I, suy ra \(\widehat{IAB}=\widehat{IDA}\)
Vậy nên ta có: \(\widehat{KBA}+\widehat{IAB}=\widehat{KAB}+\widehat{IDA}=90^o\left(\widehat{DKA}=90^o\right)\)
Gọi giao điểm của BC và AI là J.
Xét tam giác ABJ có \(\widehat{JBA}+\widehat{JAB}=90^o\Rightarrow\widehat{BJA}=90^o\)
Vậy nên \(AI\perp BC.\)
b) Ta thấy ngay \(DE=2AI;BC=2AK\)
Mà theo quan hệ giữa đường vuông góc và đường xiên thì \(AI\ge AK\)
Vậy nên \(DE\ge BC\).
1 tháng 7 2023
a:
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
góc OAC+góc AED=90 độ
=>góc OAC+góc AHD=90 độ
=>góc OAC+góc ABC=90 độ
=>góc OAC=góc OCA
=>OA=OC và góc OBA=góc OAB
=>OA=OB=OC
=>O là trung điểm của BC
b: góc KAB+góc OAB=90 độ
gócHAB+góc OBA=90 độ
mà góc OAB=góc OBA
nên góc KAB=góc HAB
=>AB là phân giác của góc HAK
c: ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC