Một hỗn hợp gồm 2 ankan X và Y là đồng đẳng kế tiếp nhau có khối lượng 10,2 gam.Đốt cháy hoàn toàn hỗn hợp cần 36,8 gam O2. Tìm CTPT của 2 ankan, Tính % khối lượng mỗi ankan trong hỗn hợp?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 2 2022
Gọi công thức chung của X, Y là CnH2n+2
\(n_{O_2}=\dfrac{36,8}{32}=1,15\left(mol\right)\)
PTHH: CnH2n+2 + \(\dfrac{3n+1}{2}\)O2 --to--> nCO2 + (n+1)H2O
\(\dfrac{2,3}{3n+1}\)<-----1,15
=> \(M_{C_nH_{2n+2}}=14n+2=\dfrac{10,2}{\dfrac{2,3}{3n+1}}\left(g/mol\right)\)
=> n = 3,5
Mà X,Y là 2 ankan kế tiếp nhau
=> X, Y là C3H8 và C4H10
Gọi số mol C3H8 và C4H10 là a, b (mol)
PTHH: C3H8 + 5O2 --to--> 3CO2 + 4H2O
a--->5a---------->3a----->4a
2C4H10 + 13O2 --to--> 8CO2 + 10H2O
b------->6,5b--------->4b------>5b
=> \(\left\{{}\begin{matrix}44a+58b=10,2\\5a+6,5b=1,15\end{matrix}\right.\)
=> a = 0,1; b = 0,1
=> \(\left\{{}\begin{matrix}m_{C_3H_8}=0,1.44=4,4\left(g\right)\\m_{C_4H_{10}}=0,1.58=5,8\left(g\right)\end{matrix}\right.\)
\(n_{CO_2}=3a+4b=0,7\left(mol\right)\)
=> \(m_{CO_2}=0,7.44=30,8\left(g\right)\)
\(m_{H_2O}=\left(4a+5b\right).18=16,2\left(g\right)\)
4 tháng 7 2017
Dùng pp bảo toàn nguyên tố Oxi và bảo toàn khối lượng.
Gọi a = n(CO2) ; b = n(H2O).
Ta có: 44a + 18b = m(ankan) + m(O2) = 47 (g).
Áp dụng BT nguyên tố Oxi:
2a + b = 36,8/32 * 2 = 2,3.
Giải hệ 2 pt trên tìm được a = 0,7 ; b = 0,9.
==> m(CO2) = 30,8 (g) ; m(H2O) = 16,2 (g).
TP
23 tháng 7 2021
Gọi công thức chung của 2 ankan trong A : \(C_nH_{2n+2}\)
PTHH: \(C_nH_{2n+2}+\dfrac{3n+1}{2}O_2\rightarrow nCO_2+\left(n+1\right)H_2O\)
\(n_{O_2}=\dfrac{36,8}{32}=1,15\left(mol\right)\)
Theo PT ta có : \(n_{C_nH_{2n+2}}=1,15:\dfrac{3n+1}{2}\left(mol\right)\)
=> \(\dfrac{10,2}{14n+2}=1,15:\dfrac{3n+1}{2}\)
=> n=3,5
=> nhhakan = \(\dfrac{10,2}{14.3,5+2}=0,2\left(mol\right)\)
Vì hỗn hợp A gồm 2 ankan là đồng đẳng kế tiếp.
=> 2 ankan cần tìm là C3H8 và C4H10
Gọi x, y lần lượt là số mol của C3H8 và C4H10
=> \(\left\{{}\begin{matrix}x+y=0,2\\44x+58y=10,2\end{matrix}\right.\)
=> x=0,1 , y=0,1
Vì thành phần phần trăm thể tích trong A cũng là thành phần phần trăm số mol trong A.
=> \(\%V_{C_3H_8}=\dfrac{0,1}{0,2}.100=50\%\)
\(\%V_{C_4H_{10}}=\dfrac{0,1}{0,2}.100=50\%\)
H
28 tháng 2 2021
CTTQ của ankan : \(C_nH_{2n+2}\)
\(n_{O_2} = \dfrac{2,24.2}{0,082.(0+273)} = 0,2(mol)\\ C_nH_{2n+2} + \dfrac{3n+1}{2}O_2 \xrightarrow{t^o} nCO_2 + (n+1)H_2O\\ n_{ankan} = \dfrac{2}{3n+1}n_{O_2} = \dfrac{0,4}{3n+1}(mol)\\ \Rightarrow \dfrac{0,4}{3n+1}.(14n+2) = 1,76\\ \Rightarrow n = 3\)
Vậy CTPT hai ankan là : \(C_2H_6,C_4H_{10}\)
3 tháng 2 2023
a) \(n_{O_2}=\dfrac{21,056}{22,4}=0,94\left(mol\right)\)
\(n_{CaCO_3}=\dfrac{52}{100}=0,52\left(mol\right)\)
BTNT C: \(n_C=n_{CO_2}=n_{CaCO_3}=0,52\left(mol\right)\)
BTNT O: \(n_{H_2O}=2n_{O_2}-2n_{CO_2}=0,84\left(mol\right)\)
\(\Rightarrow n_{ankan}=n_{H_2O}-n_{CO_2}=0,32\left(mol\right)\)
\(\Rightarrow\text{Số }\overline{C}_{\text{trung bình}}=\dfrac{n_C}{n_{ankan}}=\dfrac{0,52}{0,32}=1,625\)
Vì 2 ankan liên tiếp nhau trong dãy đồng đẳng nên 2 ankan là CH4 (metan) và C2H6 (etan)
b) BTNT H: \(n_H=2n_{H_2O}=1,68\left(mol\right)\)
Gọi \(\left\{{}\begin{matrix}n_{CH_4}=a\left(mol\right)\\n_{C_2H_6}=b\left(mol\right)\end{matrix}\right.\left(a,b>0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}n_C=n_{CH_4}+2n_{C_2H_6}=a+2b=0,52\\n_H=4n_{CH_4}+6n_{C_2H_6}=4a+6b=1,68\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0,12\\b=0,2\end{matrix}\right.\left(TM\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{CH_4}=\dfrac{0,12.16}{0,12.16+0,2.30}.100\%=24,24\%\\\%m_{C_2H_6}=100\%-24,24\%=75,76\%\end{matrix}\right.\)
c)
\(CH_4+Cl_2\xrightarrow[]{askt}CH_3Cl\left(\text{metyl clorua}\right)+HCl\\ C_2H_6+Cl_2\xrightarrow[]{askt}C_2H_5Cl\left(\text{etyl clorua}\right)+HCl\)
24 tháng 5 2018
Đáp án A
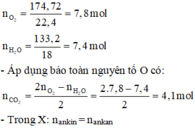
=> Quy đổi X tương đương với hỗn hợp chỉ gồm anken và amin no, đơn chức, mạch hở.
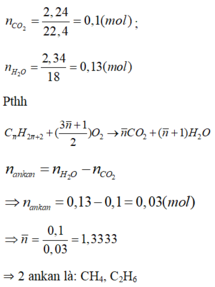
\(CT:C_{\overline{n}}H_{2\overline{n}+2}\)
\(n_{O_2}=\dfrac{36.8}{32}=1.15\left(mol\right)\)
\(\)\(C_{\overline{n}}H_{2\overline{n}+2}+\dfrac{3\overline{n}+1}{2}O_2\underrightarrow{t^0}nCO_2+\left(n+1\right)H_2O\)
\(\dfrac{2.3}{3\overline{n}+1}........1.15\)
\(M=\dfrac{10.2}{\dfrac{2.3}{3\overline{n}+1}}=\dfrac{102}{23}\left(3\overline{n}+1\right)\)
\(\Rightarrow14\overline{n}+2=\dfrac{102}{23}\cdot\left(3\overline{n}+1\right)\)
\(\Rightarrow\overline{n}=3.5\)
\(CT:C_3H_8\left(amol\right),C_4H_{10}\left(bmol\right)\)
\(m=44a+58b=10.2\left(g\right)\left(1\right)\)
\(n_{O_2}=5a+6.5b=1.15\left(2\right)\)
\(\left(1\right),\left(2\right):\)
\(a=b=0.1\)
\(\%C_3H_8=\dfrac{4.4}{10.2}\cdot100\%=43.13\%\)
\(\%C_4H_{10}=56.84\%\)