Cho hàm số bậc nhất y=-2x+5
a, hàm số đã cho đồng biến hay nghịch biến R? Vì sao?
b, vẽ đồ thị hàm số trên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hàm số y = (2 - a)x + a, biết đồ thị hàm số đi qua điểm M (3;1), hàm số đồng biến hay nghịch biến trên R==========hàm số y = (2 - a)x + a, biết đồ thị hàm số đi qua điểm M (3;1)<=>1=(2-a)3+a<=>1=6-3a +a<=>2a =5<=>a =5/2=>y=-1/2x+5/2a =-1/2<0=> nghịch biến trên R

c: Thay x=1 và y=1 vào hàm số, ta được:
y=2x1-3=-1<>1
Vậy: Điểm M ko thuộc đồ thị
b: Hàm số đồng biến vì a=2>0

a) - Với hàm số y = 2x
Bảng giá trị:
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua gốc tọa độ và điểm A( 1;2)
- Với hàm số y = -2x
Bảng giá trị:
| x | 0 | 1 |
| y = -2x | 0 | -2 |
Đồ thị hàm số y = -2x đi qua gốc tọa độ và điểm B( 1; - 2)
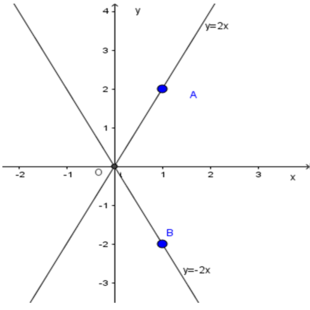
b) - Ta có O ( x 1 = 0 , y 1 = 0 ) và A( x 2 = 1 , y 2 = 2 ) thuộc đồ thị hàm số y = 2x, nên với x 1 < x 2 ta được f ( x 1 ) < f ( x 2 ) .
Vậy hàm số y = 2x đồng biến trên R.
- Lại có O( x 1 = 0 , y 1 = 0 ) và B ( x 3 = 1 , y 3 = - 2 ) thuộc đồ thị hàm số y = -2x, nên với x 1 < x 3 ta được f ( x 1 ) < f ( x 3 ) .
Vậy hàm số y = -2x nghịch biến trên R.

Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)

Câu a :))
Hàm số đã cho đồng biến .
giải thích :
Do \(m^2\ge0\forall m\)
\(\Rightarrow m^2+1>0\)
Vậy hàm số trên đồng biến.
Giả sử đths đi qua điểm cố định ( x0;y0 )
Ta có y0 = ( m2 +1 )x0 - 1
<=> y0 = m2 x0 +x0 -1
<=> y0 -x0 +1 -m2x0 = 0
Để pt nghiệm đúng với mọi m \(\Leftrightarrow\hept{\begin{cases}y_0-x_0+1=0\\x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}y_0=-1\\x_0=0\end{cases}}}\)
Vậy đths luôn đi qua điểm cố định ( 0 ; -1 )
a: Hàm số này nghịch biến vì -2<0