Với giá trị các ô D1=20, D2=30, D3=10. Hãy cho biết kết quả của công thức =Min (D1: D3, 40) là giá trị nào sau đây?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 7 2021
1)
Phương trình hoành độ giao điểm của (d1) với (d2) là:
2x+2=-x+2
nên x=0
Thay x=0 vào (d1), ta được:
y=2x+2=2
Vậy: A(0;2)
Thay y=0 vào (d1), ta được:
2x+2=0
nên 2x=-2
hay x=-1
Vậy: B(-1;0)
Thay y=0 vào (d2), ta được:
-x+2=0
hay x=2
Vậy: C(2;0)
VT
6 tháng 1 2019
Đáp án A
x12 = x1 + x2; x23 = x2 + x3
Do dao động D1 ngược pha với D3 nên dao động D1 cùng pha với –D3 có nghĩa là cùng pha với D1-3 =>
Từ giản đồ véc tơ ta có:
23 tháng 8 2021
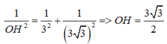
\(\left(d_1\right):y=-x+1\)
\(\left(d_2\right):y=x-1\)
\(\left(d_3\right):y=\dfrac{k+1}{1-k}x+\dfrac{k+1}{k-1}\)
a) Để (d1) và (d3) vuông góc với nhau:
\(\Leftrightarrow\left(-1\right)\left(\dfrac{k+1}{1-k}\right)=-1\)\(\Leftrightarrow k=0\)(thỏa)
Vậy k=0
b)Giao điểm của (d1) và (d2) là nghiệm của hệ \(\left\{{}\begin{matrix}y=-x+1\\y=x-1\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\)
Để (d1);(d2);(d3) đồng quy\(\Leftrightarrow\) (d3) đi qua điểm (1;0)
\(\Rightarrow0=\dfrac{k+1}{1-k}.1+\dfrac{k+1}{k-1}\)\(\Leftrightarrow0=0\)(lđ)
Vậy với mọi k thì (d1);d2);(d3) luôn cắt nhau tại một điểm
c)Gỉa sử \(M\left(x_0;y_0\right)\) là điểm cố định mà (d3) luôn đi qua
Khi đó \(\left(k+1\right)x_0+\left(k-1\right)y_0=k+1\) luôn đúng với mọi k
\(\Leftrightarrow k\left(x_0+y_0-1\right)+x_0-y_0-1=0\) luôn đúng với mọi k
\(\Leftrightarrow\left\{{}\begin{matrix}x_0+y_0-1=0\\x_0-y_0-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=1\end{matrix}\right.\)
Vậy \(M\left(2;1\right)\) là điểm cố định mà (d3) luôn đi qua.
VT
24 tháng 10 2018
Đáp án A
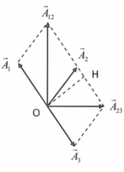
Từ dữ kiện đã cho ở đề bài, vẽ giản đồ vecto như hình vẽ, với:
+ Dao động tổng hợp x12 được biểu diễn bằng vecto
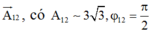
+ Dao động tổng hợp x23 được biểu diễn bằng vecto
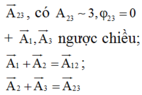
Với tam giác vuông được tạo bởi các cạnh A12 và A23, ta thấy:
VT
2 tháng 4 2019
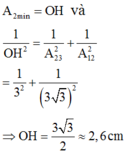
Chọn đáp án A
Ta có: x 12 = x 1 + x 2 = 3 3 ∠ π 2 1 x 23 = x 2 + x 3 = 3 ∠ 0 2 → 1 , 2 x 1 − x 3 = 6 ∠ 2 π 3 3
Vì x 1 và x 2 ngược pha nhau nên: x 1 x 3 = − A 1 A 3 ⇒ x 1 = − A 1 A 3 x 3 4
Thay (4) vào (3) ta có: − A 1 A 3 x 3 − x 3 = 6 ∠ 2 π 3 = 6 cos ω t + 2 π 3
⇔ A 1 A 3 x 3 + x 3 − 6 cos ω t + 2 π 3 = 6 cos ω t − π 3 5
Lại có: x 3 = A 3 cos ω t + φ 3 → 5 A 1 A 3 . A 3 cos ω t + φ 3 + A 3 cos ω t + φ 3 = 6 cos ω t − π 3
⇒ φ 3 = − π 3 ⇒ x 3 = A 3 cos ω t − π 3
ta có: x 3 = A 3 cos ω t + φ 3 → 5 A 1 A 3 . A 3 cos ω t + φ 3 + A 3 cos ω t + φ 3 = 6 cos ω t − π 3
⇒ A 2 2 = A 3 2 + 3 2 − 2.3. A 3 . 1 2 = A 3 2 − 2 A 3 . 3 2 + 9 4 + 27 4 = A 3 − 3 2 2 + 27 4
Nhận thấy A 2 m i n ⇔ A 3 − 3 2 2 = min = 0 ⇒ A 2 2 = 27 4 ⇒ A 2 = 3 3 2 c m
VT
9 tháng 10 2019
Chọn đáp án A
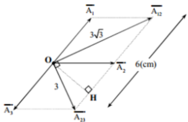
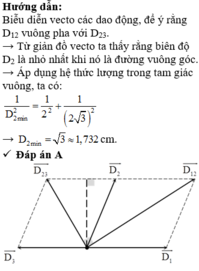
Cách 1:
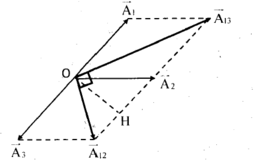
Xây dựng giãn đồ vectơ như hình vẽ.
Ta thấy vectơ A 2 → đạt giá trị nhỏ nhất khi và chỉ khi vectơ A 2 → trùng với OH.
Áp dụng hệ thức lượng trong tam giác vuông 1 O H 2 = 1 3 2 + 1 3 3 2 ⇒ O H = 3 3 2 c m
⇒ A 2 min = O H = 3 3 2 ≈ 2 , 6 c m
Cách 2. Biến đổi đại số.
x 12 = x 1 + x 2 x 23 = x 2 + x 3 x 1 x 3 = − A 1 A 3 ⇒ x 12 = x 1 + x 2 x 23 = x 2 − A 3 A 1 x 1 ⇒ ⏟ x 3 x 2 = x 23 + A 3 A 1 x 12 1 + A 3 A 1
(Mục đích của chúng ta là tìm phương trình x 2 theo x 12 và x 23 bằng cách khử x 1 và x 3 ).
Hàm x 2 được ghi lại x 2 = 3 cos ω t ⏟ x 23 + A 3 A 1 .3 3 cos ω t + π 2 1 + A 3 A 1
Nhận thấy hai phương trình x 23 và hàm đóng khung ở biểu thức trên dao động vuông pha với nhau nên biên độ của phương trình x 2 có dạng
A 2 = 1 1 + A 3 A 1 3 2 + 3 3 . A 3 A 1 2 ; Đặt A 3 A 1 = x > 0 .
⇒ A 2 = 1 1 + x 9 + 27 x 2 = 9 + 27 x 2 1 + x 2 = y ⇒ y ' = 54 x 2 + 36 x − 18 1 + x 4 = 0 ⇒ x 0 = 1 3 ⇒ A 2 = y = 9 + 27. 3 − 1 2 1 + 3 − 1 2 = 1 , 5 3 c m ≈ 2 , 6 c m
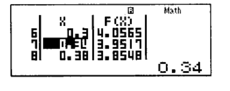
Chú ý: Có thể tìm cực trị (cũng là giá trị cực tiểu) hàm A 2 = 9 + 27 x 2 1 + x 2 bằng máy tính cầm tay FX-570VN.
Các giá trị Start và End ra dựa vào số liệu
A 12 = 3 3 c m A 23 = 3 c m ⇒ A 12 A 13 = 3 ≈ 1 , 73 A 23 = 3 thì tỉ số X = A 3 A 1 cũng sẽ nằm cỡ vào trong các khoảng từ 1 đến 10 nếu ( A 3 > A 1 ) còn nếu ( A 3 < A 1 ) thì tỉ số X ∈ 0 ; 1 . Bấm Mode 7 và nhập hàm F X = 27 + 9 x 2 1 + x 2
S t a r t = 1 E n d = 10 → E n d − S t a r t S t e p + 1 ≤ 30 S t e p ≥ 0 , 31 ⇒ S t e p = 0 , 4 (Không tìm được cực trị).
Ta chọn lại S t a r t = 0 , 1 E n d = 1 → E n d − S t a r t S t e p + 1 ≤ 30 S t e p ≥ 0 , 031 ⇒ S t e p = 0 , 04
Màn hình hiển thị ở dưới.
Chú ý:
Trong toán học khi bài toán yêu cầu tìm cực trị thì các em đạo hàm của hàm y sau đó xét y ' = 0 và lập bảng biến thiên để xét giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN). Tuy nhiên thông thường đối với bài toán vật lí hàm y có nghĩa khi nghiệm đó là nghiệm dương, khi đó đề hỏi GTLN hoặc GTNN thì khi đạo hàm của hàm y thì chỉ có duy nhất 1 nghiệm dương (tức là tồn tại GTLN thì không tồn tại GTNN và ngược lại). Dó đó chúng ta không cần vẽ bảng biến thiên mà kết luận ngay tại giá trị x 0 nào đó ( x 0 là nghiệm dương duy nhất của hàm y ' ) hàm đạt GTLN (GTNN).
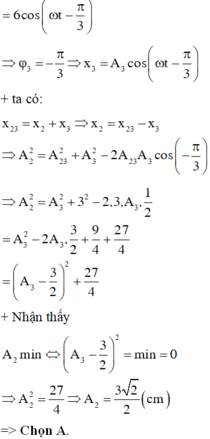
chắc là 70
Min là giá trị nhỏ nhấ mà bạn