cho đường tron tâm O, M là một điểm nằn ngoài đường tròn ,kẻ tiếp tuyến MA,MB . goi I là trung điểm của MB , IA căt O tại điểm thư 2 là K. MK căt O tại điểm thư 2 là D . chứng minh tam giác IMK đồng dạng với tam giác IAM.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

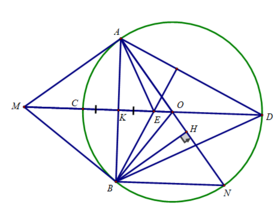
a. OM là đường trung trực của AB
⇒AM⊥AB tại H
xét ΔIAC và ΔIBA có
∠I chung
∠A=∠B=90
⇒ΔIAC ∼ ΔIBA (g.g)
⇒IA2=IB.IC
a) Vì MA,MB là tiếp tuyến \(\Rightarrow MA=MB\) và MO là phân giác \(\angle AMB\)
\(\Rightarrow OM\bot AB\)
Xét \(\Delta ICA\) và \(\Delta IAB:\) Ta có: \(\left\{{}\begin{matrix}\angle IAC=\angle IBA\\\angle BIAchung\end{matrix}\right.\)
\(\Rightarrow\Delta ICA\sim\Delta IAB\left(g-g\right)\Rightarrow\dfrac{IC}{IA}=\dfrac{IA}{IB}\Rightarrow IA^2=IB.IC\)
b) Ta có: \(IM^2=IA^2=IB.IC\Rightarrow\dfrac{IM}{IB}=\dfrac{IC}{IM}\)
Xét \(\Delta ICM\) và \(\Delta IMB:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{IM}{IB}=\dfrac{IC}{IM}\\\angle BIMchung\end{matrix}\right.\)
\(\Rightarrow\Delta ICM\sim\Delta IMB\left(c-g-c\right)\Rightarrow\angle IMC=\angle IMB=\angle BDC\)
\(\Rightarrow AM\parallel BD\)
c) Xét \(\Delta ABM\),có I là trung điểm MA,H là trung điểm AB
\(\Rightarrow IH\) là đường trung bình \(\Delta ABM\)\(\Rightarrow IH\parallel AB\)
\(\Rightarrow\angle CIH=\angle IBM=\angle CAH\Rightarrow CHAI\) nội tiếp
\(\Rightarrow\angle ACI=\angle AHI=\angle ABM=\angle BAM=\angle ABD\) \((AM\parallel BD)\)
\(=\angle ACD\)
\(\Rightarrow CA\) là phân giác 

d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB