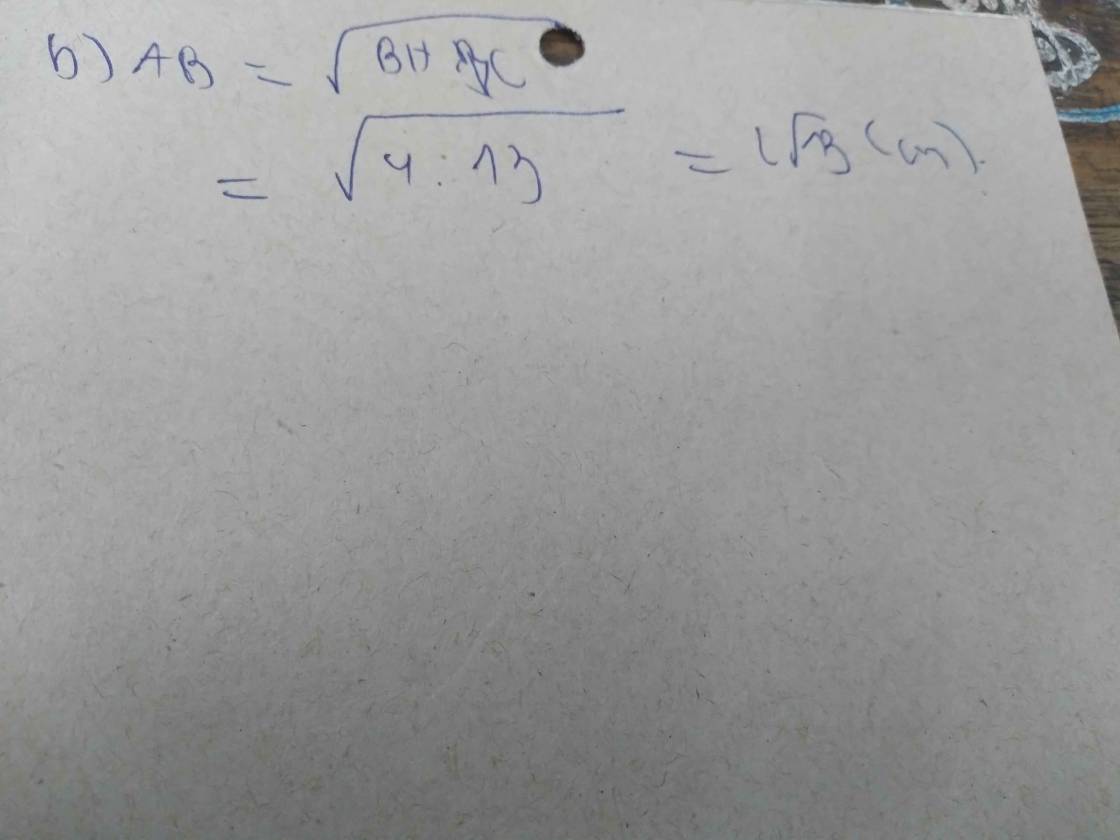Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
=>ΔABH đồng dạng với ΔCBA
b: ΔABH đồng dạng với ΔCBA
=>BA/BC=BH/BA
=>BA^2=BH*BC
=>BA=6cm

a) Xét hai tam giác ABC và HBA có:
\(\widehat{BAC}=\widehat{BHA=1V}\)
\(\widehat{ABC}\left(\widehat{HBA}\right)\): góc chung
Vậy \(\Delta\)ABC ~ \(\Delta\)HBA.
b) Ta có:
AB2 = BH . BC (vì \(\Delta\)ABC ~ \(\Delta\)HBA.)
= 4.13
= 52
\(\Rightarrow\)AB = \(\sqrt{52}=\)\(2\sqrt{13}\)(cm)
Vì \(\Delta\)ABH vuông tại H
\(\Rightarrow\)AH2 = AB2 - BH2
= 36
\(\Rightarrow\)AH = 6(cm)
c) Xét hai tam giác AHE và CHF có:
\(\widehat{HAE}=\widehat{HCF}\)(cùng phụ với \(\widehat{HAC}\))
\(\widehat{AHE}=\widehat{CHF}\) ( cùng phụ với \(\widehat{AHF}\))
Vậy \(\Delta\)AHE ~ \(\Delta\)CHF.
\(\Rightarrow\frac{AE}{CF}=\frac{AH}{CH}\Rightarrow AE.CH=AH.CF\)(đpcm)
d)

a: Xét ΔADE vuông tại E và ΔCDA vuông tại A có
góc CDA chung
=>ΔADE đồng dạng với ΔCDA
b: DE*DC=DA^2=AB^2/4
c: DB^2=DE*DC
=>DB/DE=DC/DB
=>ΔDBC đồng dạng với ΔDEB
=>góc DCB=góc DBE

a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
=>ΔABH đồng dạng với ΔCBA
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
c: Xét ΔBHI vuông tại H và ΔBAE vuông tại A có
góc ABE=góc HBI
=>ΔBHI đồng dạng với ΔBAE
d: góc AIE=góc BIH
góc AEI=góc BIH
=>góc AIE=góc AEI
=>AI=AE